Phương trình elip có dạng:
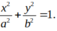
Đi qua hai điểm M; N ta được:
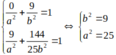
Vậy phương trình elip:
![]()
Chọn B.
Phương trình elip có dạng:
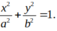
Đi qua hai điểm M; N ta được:
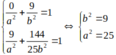
Vậy phương trình elip:
![]()
Chọn B.
C1: Trên hệ trục tọa độ Oxy, có bao nhiêu giá trị nguyên của m e [-10;10] để phương trình 2 + y ^ 2 - 2(m + 1) x + 4y + 7m + 5 = 0 là phương trình đường tròn? A.11 B.16 C.15 D.12 Câu 11 Phương trình √ x^2 -2x+4=4-x có một nghiệm là A.x=2 B.x=4 C.x=3 D. X=4
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A (-1;1) và đường thẳng
d : x - y + 1 - √2 = 0 . Viết phương trình đường tròn (C) đi qua điểm A, gốc toạ độ O và tiếp xúc với đường thẳng d .
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A (-1;1) và đường thẳng
d : x - y + 1 - √2 = 0 . Viết phương trình đường tròn (C) đi qua điểm A, gốc toạ độ O và tiếp xúc với đường thẳng d .
Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M (2;1) và đường thẳng d: x-y+1=0. Viết phương trình đường tròn đi qua M cắt d ở 2 điểm A, B phân biệt sao cho tam giác MAB vuông tại M và có diện tích bằng 2.
a) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) có phương trình 2x-3y+1=0
Lập pt đường thẳng(d') qua M(-1',1)và song song với(d)
b)Trong mặt phẳng hệ tọa độ Oxy,cho elip có pt(E):x\(\frac{x^2}{49}+\frac{y^2}{25}=1\)
tính chu vi,diện tích hình chữ nhật của elip
(3)
a) gpt: \(\sqrt{2x-3}-x+3=0\)
b) tìm các giá trị của tham số m để pt \(\sqrt{2x^2+mx-3}=x+1\) có 2 nghiệm phân biệt.
(4) trong mặt phẳng tọa độ Oxy, cho điểm I (1; -2) và 2 đg thẳng d1: 3x+y+5=0, d2: 3x+y+1=0.
a) viết phương trình đg thẳng d vuông góc với đg thẳng d1 và đi qua gốc tọa độ
b) viết pt đg thẳng đi qua 1 và cắt d1, d2 lần lượt tại A và B sao cho AB= \(2\sqrt{2}\)
giúp mk vs ạ mk cần gấp
trong mặt phẳng hệ tọa độ Oxy cho hình thang cân ABCD có hai đường chéo BD và AC vuông góc với nhau tại H và AD 2 BC. Gọi M là điểm nằm trên cạnh AB sao cho AB 3 AM N là trung điểm HC. biết B 1 3 đường thẳng HM đi qua T 2 3 đường thẳng DN có phương trình x 2y 2 0 . tìm tọa độ các điểm A,C,D
Trong mặt phẳng với hệ trục tọa độ $Oxy$, cho elip $\left( E \right)$ có phương trình: $\dfrac{{ x^2}}{9}+\dfrac{{{y}^2}}{4}=1$. Gọi ${{F}_{1}}, \, {{F}_2}$ là hai tiêu điểm của $\left( E \right)$. Tìm điểm $M$thuộc $\left( E \right)$ sao cho góc $\widehat{{{F}_{1}}M{{F}_2}}$ bằng ${{90}^{\circ}}$.
Trong hệ trục tọa đô Oxy. Cho đường tròn (C):(x-1)2+(y-2)2=5
a/Viết phương trình đường thẳng (d) đi qua gốc tọa đố và tâm của đường tròn (C)
b/Viết phương trình đường thẳng(Δ) đi qua M(1;3) cắt đường tròn (C) theo dây cung AB có độ dài bằng \(3\sqrt{2}\)
làm nhanh giúp e vs ạ
Trong mặt phẳng tọa độ Oxy, đường thẳng 2x – y = 3 đi qua điểm:
A. (0; -3) B. (2; 2) C. ( 1; 3) D. (5; 0)