Question

Trong mặt phẳng tọa độ Oxy

a) Vẽ tam giác ABC, biết A(2;4) ; B(2;-1) ; C(-4;-1)

b) Tam giác ABC là tam giác gì ? Tính diện tích của tam giác đó.

Answer 1

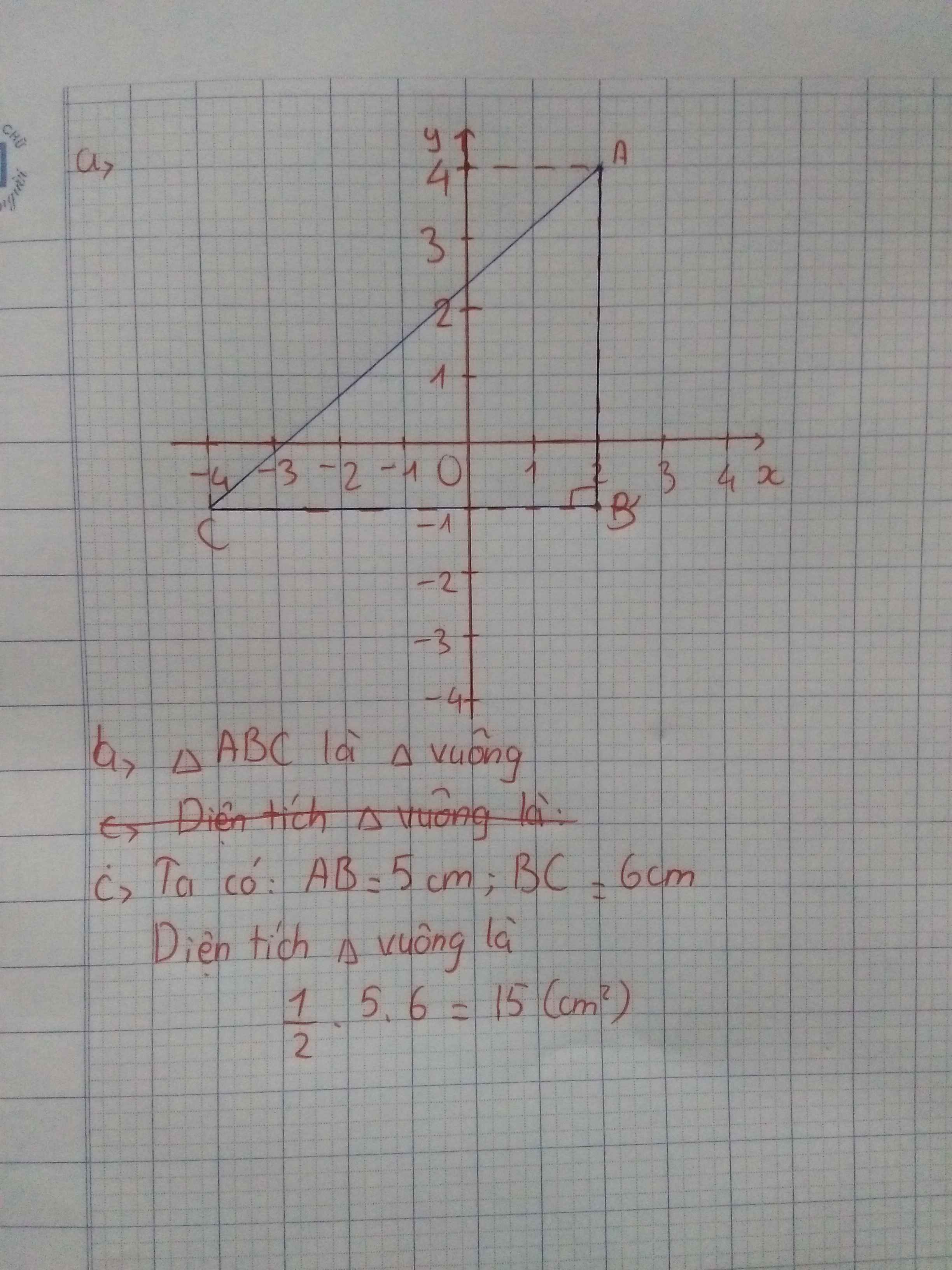
b) Độ dài đoạn thẳng AB là:

\(AB=\sqrt{\left(2-2\right)^2+\left(4+1\right)^2}=5\)

Độ dài đoạn thẳng AC là:

\(AC=\sqrt{\left(2+4\right)^2+\left(4+1\right)^2}=\sqrt{61}\)

Độ dài đoạn thẳng BC là:

\(BC=\sqrt{\left(2+4\right)^2+\left(-1+1\right)^2}=6\)

Ta có: \(BA^2+BC^2=5^2+6^2=25+36=61\)

\(AC^2=\left(\sqrt{61}\right)^2=61\)

Do đó: \(AC^2=BA^2+BC^2\)(=61)

Xét ΔABC có \(AC^2=BA^2+BC^2\)(cmt)

nên ΔABC vuông tại B(Định lí Pytago đảo)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{BA\cdot BC}{2}=\dfrac{5\cdot6}{2}=\dfrac{30}{2}=15\left(cm^2\right)\)

Answer 2

Học tốt :D