Các câu hỏi tương tự
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1;-2;2), B(-3;-2;0) và mặt phẳng (P):x+3y-z+20. Vectơ chỉ phương của đường thẳng d là giao tuyến của mặt phẳng (P) và mặt phẳng trung trực của đoạn AB có tọa độ là A.
u
→
1
;
-
1
;
0
B.
u
→
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1;-2;2), B(-3;-2;0) và mặt phẳng (P):x+3y-z+2=0. Vectơ chỉ phương của đường thẳng d là giao tuyến của mặt phẳng (P) và mặt phẳng trung trực của đoạn AB có tọa độ là
A. u → = 1 ; - 1 ; 0
B. u → = 2 ; 3 ; - 1
C. u → = 1 ; - 2 ; 0
D. u → = 3 ; - 2 ; - 3
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;1), đường cao BH có phương trình x - 3 y - 7 = 0 và trung tuyến CM có phương trình x + y + 1 = 0 . Tìm tọa độ đỉnh C
A. (-1;0)
B. (4;-5)
C. (1;-2)
D. (1;4)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân tại A có phương trình AB, AC lần lượt là
x
+
2
y
-
2
0
,
2
x
+
y
+
1
0
, điểm M (l;2) thuộc đoạn thẳng BC. Tìm tọa độ điểm D sao cho tích vô hướng
D
B
→
.
D
C...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân tại A có phương trình AB, AC lần lượt là x + 2 y - 2 = 0 , 2 x + y + 1 = 0 , điểm M (l;2) thuộc đoạn thẳng BC. Tìm tọa độ điểm D sao cho tích vô hướng D B → . D C → có giá trị nhỏ nhất
A. Không tồn tại điểm D
B. Có hai điểm D thỏa yêu cầu bài toán
C. Có một điểm D thỏa yêu cầu bài toán
D. D (0;3) hoặc D (l;2)
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;0;-1) , mặt phẳng (P): 2x+y-z-20 và mặt phẳng (Q): x-3y-40. Gọi M là một điểm nằm trên (P) và N là điểm nằm trên (Q) sao cho A là trung điểm của MN. Khi M chạy trên mặt phẳng (P) thì quỹ tích điểm N là đường thẳng d có phương trình tương ứng là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;0;-1) , mặt phẳng (P): 2x+y-z-2=0 và mặt phẳng (Q): x-3y-4=0. Gọi M là một điểm nằm trên (P) và N là điểm nằm trên (Q) sao cho A là trung điểm của MN. Khi M chạy trên mặt phẳng (P) thì quỹ tích điểm N là đường thẳng d có phương trình tương ứng là
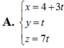
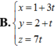
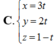
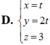
Trong không gian với hệ tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng có phương trình lần lượt là
2
x
−
2
y
−
z
0
và
x
+
3
y
+
z
−
1
0
. Tính cosin của góc giữa đường thẳng d và trục Oy. A.
3
35
B.
3
23...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng có phương trình lần lượt là 2 x − 2 y − z = 0 và x + 3 y + z − 1 = 0 . Tính cosin của góc giữa đường thẳng d và trục Oy.
A. 3 35
B. 3 23
C. 3 74
D. 3 6
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
1
;
2
;
3
và hai mặt phẳng
P
:
2
x
+
3
y
0
,
Q
:
3
x
+
4
y
0
....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 3 và hai mặt phẳng P : 2 x + 3 y = 0 , Q : 3 x + 4 y = 0 . Đường thẳng qua A song song với hai mặt phẳng P , Q có phương trình tham số là
A. x = 1 + t y = 2 + t z = 3 + t
B. x = 1 y = 2 z = t
C. x = t y = 2 z = 3 + t
D. x = 1 y = t z = 3
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y0 và (Q): 3x+4y0. Đường thẳng qua A song song với hai mặt phẳng (P); (Q) có phương trình tham số là: A.
x
t
y
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y=0 và (Q): 3x+4y=0. Đường thẳng qua A song song với hai mặt phẳng (P); (Q) có phương trình tham số là:
A. x = t y = 2 z = 3 + t
B. x = 1 y = 1 z = 3
C. x = 1 + t y = 2 + t z = 3 + t
D. x = 1 y = 2 z = t
Trong không gian với hệ tọa độ Oxyz viết phương trình đường thẳng giao tuyến của hai mặt phẳng
α
:
x
+
3
y
-
z
+
1
0
;
β
:
2
x
-
y
+
z
-
7
0
. A.
x
+
2
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz viết phương trình đường thẳng giao tuyến của hai mặt phẳng α : x + 3 y - z + 1 = 0 ; β : 2 x - y + z - 7 = 0 .
A. x + 2 2 = y - 3 = z + 3 - 7
B. x - 2 2 = y 3 = z - 3 - 7
C. x - 2 = y - 3 - 3 = z - 10 7
D. x - 2 - 2 = y 3 = z - 3 7
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2xy+10 và x+y-40 Phương trình đường thẳng AD là A. x+2y+50 B. x-2y+50 C. x+2y-70 D. x-2y-70
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng chứa các cạnh AB,AC lần lượt là 2x=y+1=0 và x+y-4=0 Phương trình đường thẳng AD là
A. x+2y+5=0
B. x-2y+5=0
C. x+2y-7=0
D. x-2y-7=0




