Question

Trong mặt phẳng tọa độ cho điểm A (-1;2) và đường thẳng (D₁): y = -2x + 3.

a) Vẽ (D₁). Điểm A có thuộc (D₁) không? Vì sao?

b) Lập phương trình đường thẳng (D₂) đi qua điểm A và song song với (D₁).

c) Tính khoảng cách giữa 2 đường thẳng (D₁) và (D₂).

Answer 1

a: Thay x=-1 và y=2 vào y=-2x+3, ta được:

\(-2\cdot\left(-1\right)+3=2\)

=>3+2=2

=>5=2(loại)

=>A không thuộc (D1)

Vẽ đồ thị:

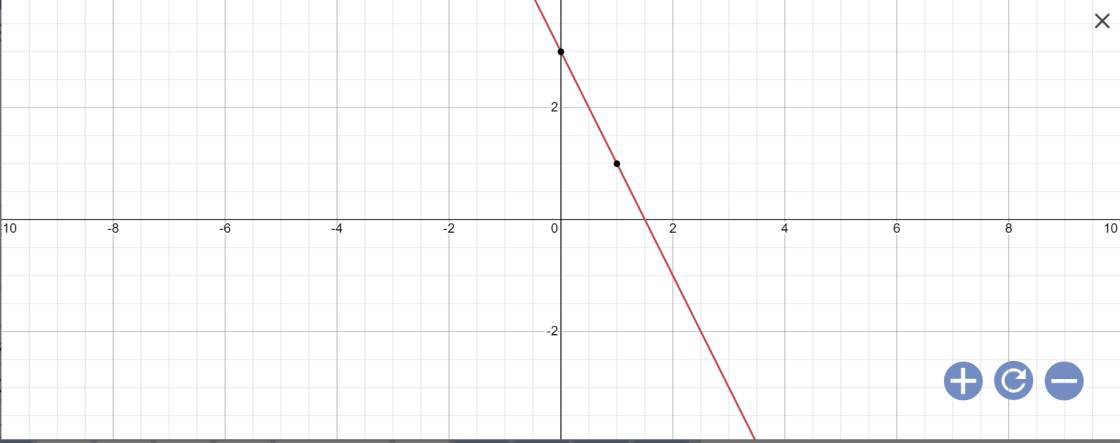
b: Gọi phương trình cần tìm là (D2): y=ax+b(\(a\ne0\))

Vì (D2)//(D1) nên \(\left\{{}\begin{matrix}a=-2\\b\ne3\end{matrix}\right.\)

Vậy: y=-2x+b

Thay x=-1 và y=2 vào y=-2x+b, ta được:

\(b-2\cdot\left(-1\right)=2\)

=>b+2=2

=>b=0(nhận)

Vậy: (D2): y=-2x

c:

(D1): y=-2x+3

=>-2x-y+3=0

=>2x+y-3=0

 A(-1;2)

Vì (D1)//(D2) nên \(d\left(\left(D1\right);\left(D2\right)\right)=d\left(A;D1\right)\)

=>\(d\left(\left(D1\right);\left(D2\right)\right)=\dfrac{\left|2\cdot\left(-1\right)+1\cdot2-3\right|}{\sqrt{2^2+1^2}}=\dfrac{3}{\sqrt{5}}\)