Đáp án C
Phương trình mặt phẳng đoạn chắn của (ABC) là
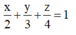
Do đó (ABC): 6x + 4y + 3z - 12 = 0
Đáp án C
Phương trình mặt phẳng đoạn chắn của (ABC) là
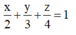
Do đó (ABC): 6x + 4y + 3z - 12 = 0
Trong không gian với hệ toạ độ Oxyz, (α) là mặt phẳng đi qua điểm A ( 2 ; - 1 ; 5 ) và vuông góc với hai mặt phẳng ( P ) : 3 x – 2 y + z – 1 = 0 v à ( Q ) : 5 x – 4 y + 3 z + 10 = 0 . Phương trình mặt phẳng (α) là:
A. x + 2y + z- 5 = 0.
B. 2x – 4y – 2z – 9 = 0.
C. x - 2y + z -1 = 0
D. x- 2y- z + 1 = 0
Trong hệ trục tọa độ Oxyz, cho phương trình mặt phẳng (P): 2x+4y-3z+1=0. Vecto pháp tuyến của (P) là:
A. (2;4;3)
B. (2;4;-3)
C. (2;-4;-3)
D. (-3;4;2)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2;1;3). Mặt phẳng (P) đi qua A và song song với mặt phẳng (Q): x+2y+3z+2=0 có phương trình là
A. x+2y+3z-9=0
B.x+2y+3z-13=0
C. x+2y+3z+5=0
D. x+2y+3z+13=0
Trong không gian với hệ tọa độ Oxyz cho hai mặt cầu ( S 1 ) , ( S 2 ) lần lượt có phương trình là x 2 + y 2 + z 2 - 2 x - 2 y - 2 z - 22 = 0 , x 2 + y 2 + z 2 - 6 x + 4 y + 2 z + 5 = 0 . Xét các mặt phẳng (P) thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Gọi M(a;b;c) là điểm mà tất cả các mp(P) đi qua. Tính tổng S=a+b+c
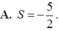
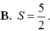
![]()
![]()
Trong không gian Oxyz. Tính thể tích V của khối đa diện giới hạn bởi
mặt phẳng (P): 2x - 4y + 3z - 24 = 0 và các mặt phẳng tọa độ.
A. V = 576
B. V= 288
C. V = 192
D. V = 96
Trong không gian với hệ trục tọa độ Oxyz, cho A ( 3 ; − 1 ; − 3 ) , B ( − 3 ; 0 ; − 1 ) , C ( − 1 ; − 3 ; 1 ) và mặt phẳng ( P ) : 2 x + 4 y + 3 z − 19 = 0 . Tọa độ M ( a , b , c ) thuộc (P) sao cho M A → + 2 M B → + 5 M C → đạt giá trị nhỏ nhất. Khi đó a+b+c bằng:
A. 4
B. 5
C. 6
D. 7
Trong hệ trục tọa độ Oxyz cho mặt phẳng (P) x-4y+3z-2=0. Một vecto pháp tuyến của (P)
A. (0;-4;3)
B. (1;4;3)
C. (-1;4;-3)

Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2; -1; 0) và mặt phẳng (P): x - 2y - 3z + 10 = 0. Phương trình mặt phẳng (Q) đi qua A và song song với mặt phẳng (P) là:
A. x - 2y + 3z + 4 = 0
B. -x + 2y + 3z + 4 = 0
C. x - 2y - 3z + 4 = 0
D. x + 2y - 3z = 0.
Trong không gian Oxyz, biết mặt phẳng ax+by+cz-24=0 qua A(1;2;3) và vuông góc với hai mặt phẳng (P): 3x-2y+z+4=0, (Q): 5x-4y+3z+1=0. Giá trị a+b+c bằng
A. 8.
B. 9.
C. 10.
D. 12.