Đáp án D
Phương pháp:
Đường thẳng
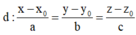
có 1 VTCP là u → = ( a ; b ; c )
Cách giải: Đường thẳng d có 1 VTCP là u → = ( 3 ; - 2 ; 1 )
Đáp án D
Phương pháp:
Đường thẳng
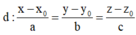
có 1 VTCP là u → = ( a ; b ; c )
Cách giải: Đường thẳng d có 1 VTCP là u → = ( 3 ; - 2 ; 1 )
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2;-1;-2) và đường thẳng d có phương trình x - 1 1 = y - 1 - 1 = z - 1 1 . Gọi (P) là mặt phẳng đi qua điểm A, song song với đường thẳng d và khoảng cách từ đường thẳng d tới mặt phẳng (P) là lớn nhất. Khi đó, mặt phẳng (P) vuông góc với mặt phẳng nào sau đây?
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d: x = 1 - t y = 2 t z = 2 + 2 t , t ∈ ℝ và mặt phẳng (P): x + y -z -1 = 0 Giao điểm M của d và (P) có tọa độ là
A. M(1;0;2)
B. M(3;−4;−2)
C. M(0;2;4)
D. M(1;1;1)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-4;1;3) và đường thẳng d : x + 1 - 2 = y - 1 1 = z + 3 3 . B là điểm có tọa độ nguyên trên d sao cho A B = 5 . Tìm tọa độ điểm B.
![]()
![]()

![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 1 2 = y 3 = z + 1 - 1 và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là:
A . x - 3 2 = y 2 = z + 5 - 1
B . x - 1 = y + 2 3 = z 4
C . x + 2 3 = y 1 = z - 1 - 1
D. Tất cả sai
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(-2;-2;1), A(1;2;-3) và đường thẳng d: x + 1 2 = y - 5 2 = z - 1 . Tìm vectơ chỉ phương u → của dường thẳng ∆ đi qua M, vuông góc với đường thẳng d, đồng thời cách điểm A một khoảng lớn nhất
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho 2 điểm A(1;-2;3) và B(0;1;2). Đường thẳng d đi qua 2 điểm A, B có một vectơ chỉ phương là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho hai điểm A ( 1 ; - 1 ; 1 ) , B ( - 1 ; 2 ; 3 ) và đường thẳng ∆ : x + 1 - 2 = y - 2 1 = z - 3 3 . Phương trình đường thẳng d đi qua điểm A, đồng thời vuông góc với hai đường thẳng AB và Δ là
A. x - 7 1 = y - 2 - 1 = z - 4 1
B. x - 1 7 = y + 1 2 = z - 1 4
C. x + 1 7 = y - 1 - 2 = z + 1 4
D. x + 1 7 = y - 1 2 = z + 1 4
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-1), đường thẳng d : x - 1 2 = y + 1 1 = z - 2 - 1 và mặt phẳng (P): x+y+2z+1=0. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. (3;-2;-1)
B. (-3;8;-3)
C. (0;3;-2)
D. (6;-7;0)
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x 1 = y - 2 = z + 1 1 và d ' : x - 1 - 2 = y - 2 4 = z 2 . Viết phương trình mặt phẳn (Q) chứa hai đường thẳng d và d’.
![]()
![]()
![]()
![]()