Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x-y+2z-60 và điểm M(1;-1;2). Phương trình mặt cầu tâm nằm trên trục Ox và tiếp xúc với mặt phẳng (P) tại điểm M là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x-y+2z-6=0 và điểm M(1;-1;2). Phương trình mặt cầu tâm nằm trên trục Ox và tiếp xúc với mặt phẳng (P) tại điểm M là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, mặt phẳng chứa hai điểm A(1;0;1), B(-1;2;2) và song song với trục Ox có phương trình là A. y-2z+20 B. x+2z-30 C. 2y-z+10 D. x+y-z0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt phẳng chứa hai điểm A(1;0;1), B(-1;2;2) và song song với trục Ox có phương trình là
A. y-2z+2=0
B. x+2z-3=0
C. 2y-z+1=0
D. x+y-z=0
Trong không gian với hệ tọa độ Oxyz , cho hai điểm M(1;2;3) và N(2;1;−2). Phương trình mặt phẳng (P) chứa hai điểm M,N và song song với trục Ox là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz , cho hai điểm M(1;2;3) và N(2;1;−2). Phương trình mặt phẳng (P) chứa hai điểm M,N và song song với trục Ox là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) chứa trục Oy và đi qua điểm M(1;1;-1) có phương trình là A. x + z 0 B. x - y 0 C. x - z 0 D. y + z 0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) chứa trục Oy và đi qua điểm M(1;1;-1) có phương trình là
A. x + z =0
B. x - y =0
C. x - z =0
D. y + z =0
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(3;-4;7) và chứa trục Oz.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(3;-4;7) và chứa trục Oz.
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng qua A(1;2;-1) có một véc-tơ pháp tuyến (2;0;0) có phương trình là: A. y + z 0 B. y + z - 1 0 C. x - 1 0 D. 2x - 1 0.
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng qua A(1;2;-1) có một véc-tơ pháp tuyến ![]() = (2;0;0) có phương trình là:
= (2;0;0) có phương trình là:
A. y + z = 0
B. y + z - 1 = 0
C. x - 1 = 0
D. 2x - 1 = 0.
Trong không gian với hệ tọa độ Oxyz, cho điểm H(a,b,c) với a,b,c0 . Mặt phẳng (P) chứa điểm H và lần lượt cắt các trục Ox, Oy, Oz tại A, B, C thỏa mãn H là trực tâm của tam giác ABC. Phương trình của mặt phẳng (P) là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm H(a,b,c) với a,b,c>0 . Mặt phẳng (P) chứa điểm H và lần lượt cắt các trục Ox, Oy, Oz tại A, B, C thỏa mãn H là trực tâm của tam giác ABC. Phương trình của mặt phẳng (P) là
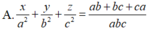
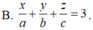
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) đi qua A(1;1;3) và chứa trục hoành có phương trình là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) đi qua A(1;1;3) và chứa trục hoành có phương trình là:
![]()
![]()
![]()
![]()




