Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, mặt phẳng chứa hai điểm A(1;0;1), B(-1;2;2) và song song với trục Ox có phương trình là A. y-2z+20 B. x+2z-30 C. 2y-z+10 D. x+y-z0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt phẳng chứa hai điểm A(1;0;1), B(-1;2;2) và song song với trục Ox có phương trình là
A. y-2z+2=0
B. x+2z-3=0
C. 2y-z+1=0
D. x+y-z=0
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y0 và (Q): 3x+4y0. Đường thẳng qua A song song với hai mặt phẳng (P) và (Q) có phương trình tham số là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y=0 và (Q): 3x+4y=0. Đường thẳng qua A song song với hai mặt phẳng (P) và (Q) có phương trình tham số là:
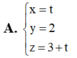
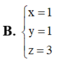
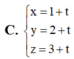
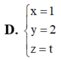
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
α
:
2
x
-
y
-
3
z
+
10
0
và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng
α
có phương trình là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng α : 2 x - y - 3 z + 10 = 0 và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng α có phương trình là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng (P): 2x+y-4z+10. Đường thẳng (d) qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số đường thẳng (d)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng (P): 2x+y-4z+1=0. Đường thẳng (d) qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số đường thẳng (d)
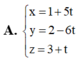
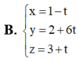
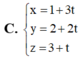
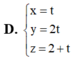
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;3) và mặt phẳng (P): 2x+y-4z+10, đường thẳng d đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;3) và mặt phẳng (P): 2x+y-4z+1=0, đường thẳng d đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.
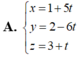
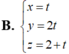
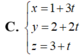
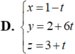
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua hai điểm A(2;1;3), B(1;-2;1) và song song với đường thẳng d
x
-
1
+
t
y
2
t...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua hai điểm A(2;1;3), B(1;-2;1) và song song với đường thẳng d x = - 1 + t y = 2 t z = - 3 - 2 t
A. 2x + y + 3z + 19 =0
B.10x - 4y + z - 19 =0
C. 2x + y + 3z - 19 =0
D. 10x - 4y + z + 19 =0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;-1;5), B(1;-2;3). Mặt phẳng
α
đi qua hai điểm A,B và song song với trục Ox có vect ơ pháp tuyến
n
→
(
0
;
a
;
b
)
. Khi đó , tỷ số
a
b
bằng A. 2 B. -2 C.
-
3
2
D.
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;-1;5), B(1;-2;3). Mặt phẳng α đi qua hai điểm A,B và song song với trục Ox có vect ơ pháp tuyến n → ( 0 ; a ; b ) . Khi đó , tỷ số a b bằng
A. 2
B. -2
C. - 3 2
D. 3 2
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;1) và B(3;1;0). Mặt phẳng (P) song song với đường thẳng AB và trục Ox có một véc tơ pháp tuyến là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;1) và B(3;1;0). Mặt phẳng (P) song song với đường thẳng AB và trục Ox có một véc tơ pháp tuyến là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P). A. 3x+2y+z+140 B. 2x+y+3z+90 C. 3x+2y+z-140 D. 2x+y+z-90.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14=0
B. 2x+y+3z+9=0
C. 3x+2y+z-14=0
D. 2x+y+z-9=0.




