Đáp án A.
Gọi:
![]()
Phương trình mặt phẳng (P) có dạng:

Vì M là trực tâm của tam giác ABC nên
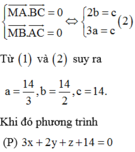
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Đáp án A.
Gọi:
![]()
Phương trình mặt phẳng (P) có dạng:

Vì M là trực tâm của tam giác ABC nên
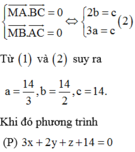
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14=0
B. 2x+y+3z+9=0
C. 3x+2y+z-14=0
D. 2x+y+z-9=0.
Trong không gian với hệ toạ độ Oxyz, gọi (α) là mặt phẳng qua G ( 1 ; 2 ; 3 ) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A,B, C (khác gốc O) sao cho G là trọng tâm của tam giác ABC. Khi đó mặt phẳng (α) có phương trình:
A. 3x + 6y + 2z + 18 = 0
B. 6x + 3y + 2z - 18 = 0
C. 2x + y + 3z - 9 = 0
D. 6x + 3y + 2z + 9 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 6x +3y-2z -6=0
B. x +2y+3z -14=0
C. x +2y+3z -11=0
D. x 1 + y 2 + z 3 = 3
Trong không gian Oxyz, viết phương trình mặt phẳng (P) qua M(1;2;3) và cắt ba trục toạ độ Ox, Oy, Oz lần lượt tại A, B, C sao cho M là trọng tâm của tam giác ABC.
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;-2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC
A. 6x - 3y -2z - 6 = 0
B. x - 2y + 3z + 14 = 0
C. x 1 + y - 2 + z 3 = 3
D. x - 2y + 3z - 14 = 0
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;2) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 2x + 2y + z - 8 = 0
B. 2x + 2y + z + 8 = 0
C. x 1 + y 2 + z 2 = 1
D. x + 2y + 2z - 9 = 0
Trong không gian Oxyz cho điểm M (2;1;5). Mặt phẳng (P) đi qua điểm M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho M là trực tâm của tam giác ABC. Tính khoảng cách từ điểm I (1;2;3) đến mặt phẳng (P)
A . 17 30 30
B . 13 30 30
C . 19 30 30
D . 11 30 30
Trong không gian Oxyz cho điểm M(2;1;5) Mặt phẳng (P) đi qua điểm M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho M là trực tâm của tam giác ABC. Tính khoảng cách từ điểm I(1;2;3) đến mặt phẳng (P)
A. 17 30 30
B. 13 30 30
C. 19 30 30
D. 11 30 30
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) đi qua gốc toạ độ và nhận ![]() =(3;2;1) là véctơ pháp tuyến. Phương trình của mặt phẳng (P) là:
=(3;2;1) là véctơ pháp tuyến. Phương trình của mặt phẳng (P) là:
A. 3x+2y+z-14=0
B. 3x+2y+z=0
C. 3x+2y+z+2=0
D. x+2y+3z=0.