Trong không gian với hệ tọa độ Oxyz, cho các điểm A − 2 ; 0 ; 0 , B 0 ; 4 ; 2 , C 2 ; 2 ; − 2 . Gọi d là đường thẳng đi qua A và vuông góc với mặt phẳng A B C , S là điểm di động trên đường thẳng d, G và H lần lượt là trọng tâm của Δ A B C , trực tâm của Δ S B C . Đường thẳng GH cắt đường thẳng d tại S'. Tính tích S A . S ' A
A. S A . S ' A = 3 2
B. S A . S ' A = 9 2
C. S A . S ' A = 12
D. S A . S ' A = 6
Đáp án C
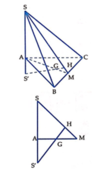
Nhận thấy A B = B C = C A = 2 6 nên Δ A B C đều. Do G là trọng tâm của Δ A B C nên C G ⊥ A B , mà C G ⊥ S A ⇒ C G ⊥ S A B ⇒ C G ⊥ S B . Lại có C H ⊥ S B (H là trực tâm của Δ S B C ) nên S B ⊥ C H G . Suy ra S B ⊥ G H .
Gọi M là trung điểm của BC.
Ta có
B C ⊥ S A , B C ⊥ A M ⇒ B C ⊥ S A M ⇒ B C ⊥ G H .
Như vậy G H ⊥ S B C ⇒ G H ⊥ S M hay S ' H ⊥ S M ⇒ S S ' H ^ = S M A ^ .
Suy ra Δ A S ' G ∽ Δ A M S ⇒ A S ' A M = A G A S
⇒ A S ' . A S = A M . A G = A M . 2 3 A M = 2 3 . A B 3 2 2 = 2 3 . 2 6 . 3 2 = 12.



