Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng P , Q và R lần lượt có phương trình P : x + m y - z + 2 = 0 ; Q : m x - y + z + 1 = 0 và R : 3 x + y + 2 z + 5 = 0 . Gọi d m là giao tuyến của hai mặt phẳng P và Q . Tìm m ra để đường thẳng vuông góc với mặt phẳng R
A. m = 1 m = - 1 3
B. m = 1
C. m = - 1 3
D. Không có m
Chọn đáp án D
Mặt phẳng (P) có vec-tơ pháp tuyến là n P ⇀ = 1 ; m ; - 1
Mặt phẳng (Q) có vec-tơ pháp tuyến là n Q ⇀ = m ; - 1 ; 1
Đường thẳng d m là giao tuyến của hai mặt phẳng (P) và (Q) nên có một vec- tơ chỉ phương là
![]()
Mặt phẳng (P) có vec-tơ pháp tuyến là n R ⇀ = 3 ; 1 ; 2
Để d m ⊥ R ⇔ Hai vec-tơ u ⇀ và n R ⇀ cùng phương
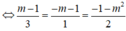
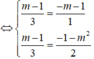
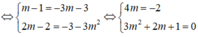
⇒ Không tồn tại giá trị m thỏa mãn yêu cầu bài toán.



