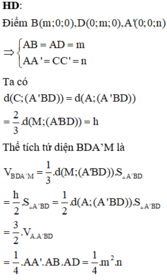Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxy, cho hình hộp chữ nhật ABCD.ABCD có A trùng với gốc tọa độ O, các đỉnh
B
m
;
0
;
0
,
D
0
;
m
;
0
,
A
0
;
0...
Đọc tiếp
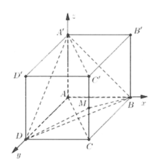
Trong không gian với hệ tọa độ Oxy, cho hình hộp chữ nhật ABCD.A'B'C'D' có A trùng với gốc tọa độ O, các đỉnh B m ; 0 ; 0 , D 0 ; m ; 0 , A ' 0 ; 0 ; n với m , n > 0 và m + n = 4 . Gọi M là trung điểm của cạnh CC'. Khi đó thể tích tứ diện BDA'M đạt giá trị lớn nhất bằng:
A. 245 108
B. 9 4
C. 64 27
D. 75 32
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(-2;0;0),B(0;-2;0),C(0;0;-2). Các điểm M, N, P lần lượt trên ba cạnh OA, OB, OC sao cho
O
A
O
M
+
O
B
O
N
+
O
C
O
P
4...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(-2;0;0),B(0;-2;0),C(0;0;-2). Các điểm M, N, P lần lượt trên ba cạnh OA, OB, OC sao cho O A O M + O B O N + O C O P = 4 và khối tứ diện OMNP có thể tích nhỏ nhất. Mặt phẳng ( α ) :ax+by+cz-1=0 đi qua ba điểm M, N, P. Tính S=a+b+c.
A. S = - 9 2
B. S = -4
C. S = -2
D. S = -3
Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD với A(3;5;-1),B(0;-1;8),C(-1;-7;3),D(1;0;2) và điểm M(1;1;5). Mặt phẳng (P):ax+by+cz-14=0 qua hai điểm D,M cắt cạnh AC và (P) chia khối tứ diện ABCD thành hai phần có thể tích bằng nhau. Giá trị của biểu thức a+b+c bằng
A. 10
B. 16
C. 8
D. -36
Trong không gian Oxyz, cho các điểm
M
(
0
;
0
;
0
)
,
N
(
0
;
n
;
0
)
,
P
(
0
;
0
;
p
)
không trùng với gốc tọa độ và thỏa mãn
m
2
+
n
2
+
p
2...
Đọc tiếp
Trong không gian Oxyz, cho các điểm M ( 0 ; 0 ; 0 ) , N ( 0 ; n ; 0 ) , P ( 0 ; 0 ; p ) không trùng với gốc tọa độ và thỏa mãn m 2 + n 2 + p 2 = 3 . Tìm giá trị lớn nhất của khoảng cách từ điểm O đến mặt phẳng (MNP)
A . 1 3 .
B . 3 .
C . 1 3 .
D . 1 27 .
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADDA. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng A.
3
5
4
14
B.
14...
Đọc tiếp
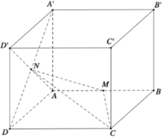
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A'. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
A. 3 5 4 14
B. 14 4
C. 3 14 4 5
D. 9 4 14
Trong không gian Oxyz, cho đường thẳng
d
:
x
4
-
3
t
y
3
+
4
t
z...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d : x = 4 - 3 t y = 3 + 4 t z = 0 . Gọi A là hình chiếu vuông góc của O trên d. Điểm M di động trên tia Oz, điểm N di động trên đường thẳng d sao cho MN = OM + AN. Gọi I là trung điểm của đoạn thẳng OA. Trong trường hợp diện tích tam giác IMN đạt giá trị nhỏ nhất, một vectơ pháp tuyến của mặt phẳng (M, d) có tọa độ là
A. 4 ; 3 ; 5 2
B. 4 ; 3 ; 10 2
C. 4 ; 3 ; 5 10
D. 4 ; 3 ; 10 10
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;0;-1) , mặt phẳng (P): 2x+y-z-20 và mặt phẳng (Q): x-3y-40. Gọi M là một điểm nằm trên (P) và N là điểm nằm trên (Q) sao cho A là trung điểm của MN. Khi M chạy trên mặt phẳng (P) thì quỹ tích điểm N là đường thẳng d có phương trình tương ứng là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;0;-1) , mặt phẳng (P): 2x+y-z-2=0 và mặt phẳng (Q): x-3y-4=0. Gọi M là một điểm nằm trên (P) và N là điểm nằm trên (Q) sao cho A là trung điểm của MN. Khi M chạy trên mặt phẳng (P) thì quỹ tích điểm N là đường thẳng d có phương trình tương ứng là
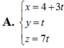
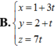
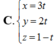
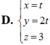
Trong không gian với hệ tọa độ Oxyz, xét tứ diện ABCD có các cặp cạnh đối diện bằng nhau và điểm D khác phía với O so với mặt phẳng (ABC); đồng thời A, B, C lần lượt là giao điểm của các trục Ox, Oy, Oz và mặt phẳng
α
:
x
m
+
y
m
+
2
+
z
m
-
5...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, xét tứ diện ABCD có các cặp cạnh đối diện bằng nhau và điểm D khác phía với O so với mặt phẳng (ABC); đồng thời A, B, C lần lượt là giao điểm của các trục Ox, Oy, Oz và mặt phẳng α : x m + y m + 2 + z m - 5 = 1 (với m ≠ - 2 , m ≠ 0 , m ≠ 5 ). Tìm khoảng cách ngắn nhất từ tâm mặt cầu ngoại tiếp I của tứ diện ABCD đến O.
A. 20
B. 1 4
C. 36
D. 26 2
Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c 2. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P). A. 2017 B.
2014
3
C.
2016
3
D.
2015...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c = 2. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P).
A. 2017
B. 2014 3
C. 2016 3
D. 2015 3