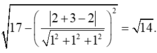Các câu hỏi tương tự
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
-
1
)
2
+
(
z
-
1
)
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 1 và điểm A(2;2;2). Xét các điểm M thuộc (S) sao cho đường thẳng AM luôn tiếp xúc với (S). M luôn thuộc một mặt phẳng cố định có phương trình là
![]()
![]()
![]()
![]()
Trong mặt phẳng tạo độ Oxyz, cho bốn điểm A(0;-1;2), B(2;-3;0), C(-2;1;1), D(0;-1;3). Gọi (L) là tập hợp tất cả các điểm M trong không gian thỏa mãn đẳng thức
M
A
→
.
M
B
→
M
C
→
.
M
D
→
1...
Đọc tiếp
Trong mặt phẳng tạo độ Oxyz, cho bốn điểm A(0;-1;2), B(2;-3;0), C(-2;1;1), D(0;-1;3). Gọi (L) là tập hợp tất cả các điểm M trong không gian thỏa mãn đẳng thức M A → . M B → = M C → . M D → = 1 . Biết rằng (L) là một đường tròn, đường tròn đó có bán kính r bằng bao nhiêu?
A. r = 11 2
B. r = 7 2
C. r = 3 2
D. r = 5 2
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
+
1
2
+
y
+
2
2
+
z
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x + 1 2 + y + 2 2 + z 2 = 4 và các điểm A(-2;0;-2 2 ), B(-4;-4;0). Biết rằng tập hợp các điểm M thuộc (S) và thỏa mãn M A 2 + M O → . M B → = 16 là một đường tròn. Tính bán kính đường tròn đó.
A. 3 2 4 .
B. 3 2 .
C. 3 7 4 .
D. 5 2 .
Trong không gian Oxyz, cho các điểm A(4;-2;4), B(-2;6;4), C(5;-1;-6). Xét các điểm M thuộc mặt phẳng (Oxy) sao cho
A
M
B
^
90
°
, đoạn thẳng CD có độ dài lớn nhất bằng A.
73
B.
5
3
C. 10 D. 8
Đọc tiếp
Trong không gian Oxyz, cho các điểm A(4;-2;4), B(-2;6;4), C(5;-1;-6). Xét các điểm M thuộc mặt phẳng (Oxy) sao cho A M B ^ = 90 ° , đoạn thẳng CD có độ dài lớn nhất bằng
A. 73
B. 5 3
C. 10
D. 8
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;0;2) ; N(1;-1;-1) và mặt phẳng (P): x + 2y - z + 2 0. Một mặt cầu đi qua M ; N tiếp xúc với mặt phẳng (P) tại điểm E . Biết E luôn thuộc một đường tròn cố định, tính bán kính đường tròn đó.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;0;2) ; N(1;-1;-1) và mặt phẳng (P): x + 2y - z + 2 = 0. Một mặt cầu đi qua M ; N tiếp xúc với mặt phẳng (P) tại điểm E . Biết E luôn thuộc một đường tròn cố định, tính bán kính đường tròn đó.
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²25 và hai điểm A (3;-2;6), B (0;1;0). Mặt phẳng (P):ax+by+cz-20 chứa đường thẳng AB và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính giá trị của biểu thức M2a+b-c. A. M2. B. M3. C. M1. D. M4.
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=25 và hai điểm A (3;-2;6), B (0;1;0). Mặt phẳng (P):ax+by+cz-2=0 chứa đường thẳng AB và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính giá trị của biểu thức M=2a+b-c.
A. M=2.
B. M=3.
C. M=1.
D. M=4.
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1 0, (Q): 2x + y + z - 1 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu. A.
r
3
B.
r
3...
Đọc tiếp
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng
(
α
)
:
2
x
+
2
y
+
z
-
12
0
Điểm M di động trên mặt phẳng
(
α
)
sao cho MA, MB luôn tạo với ...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng ( α ) : 2 x + 2 y + z - 12 = 0 Điểm M di động trên mặt phẳng ( α ) sao cho MA, MB luôn tạo với ( α ) các góc bằng nhau. Biết rằng M luôn thuộc một đường tròn ( ω ) cố định. Hoành độ của tâm đường tròn ( ω ) bằng
A. 9 2
B. 2
C. 10
D. -4
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
(
P
)
:
x
−
y
+
2
z
+
1
0
và
(
Q
)
:
2
x
+
y
+
z
−
z
0.
Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : x − y + 2 z + 1 = 0 và ( Q ) : 2 x + y + z − z = 0. Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính r. Xác định r sao cho chỉ có duy nhất một mặt cầu (S) thỏa mãn điều kiện bài toán
A. r = 3 2 2 .
B. r = 10 2 .
C. r = 3 .
D. r = 14 2 .