Các câu hỏi tương tự
Trong không gian Oxyz, cho điểm A(1;−3;0) và mặt cầu (S):
(
x
-
2
)
2
+
(
y
+
6
)
2
+
z
2
50
tâm I. Xét các điểm M thuộc (S) sao cho góc
∠
A
M...
Đọc tiếp
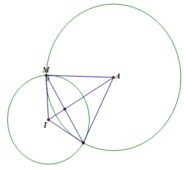
Trong không gian Oxyz, cho điểm A(1;−3;0) và mặt cầu (S): ( x - 2 ) 2 + ( y + 6 ) 2 + z 2 = 50 tâm I. Xét các điểm M thuộc (S) sao cho góc ∠ A M I lớn nhất, M luôn thuộc mặt phẳng có phương trình là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
x
+
2
2
16
và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi
P
m
là mặt phẳng chứa các tiếp điểm, biết ...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + x + 2 2 = 16 và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi P m là mặt phẳng chứa các tiếp điểm, biết P m luôn đi qua một đường thẳng d cố định, phương trình đường thẳng d là:
A. 
B. 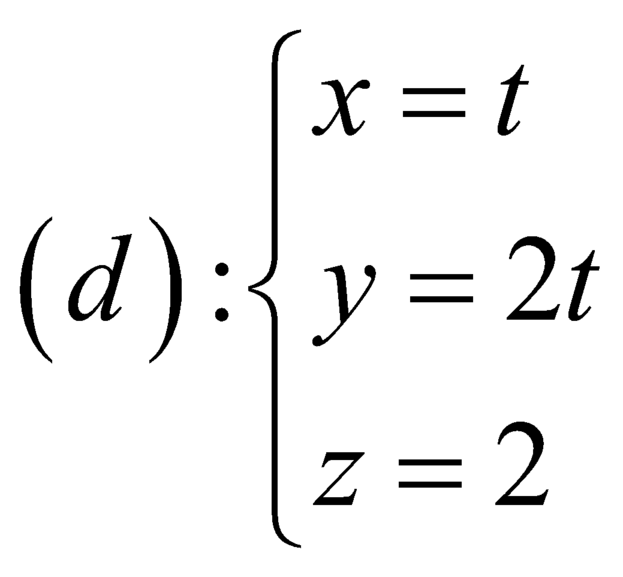
C. 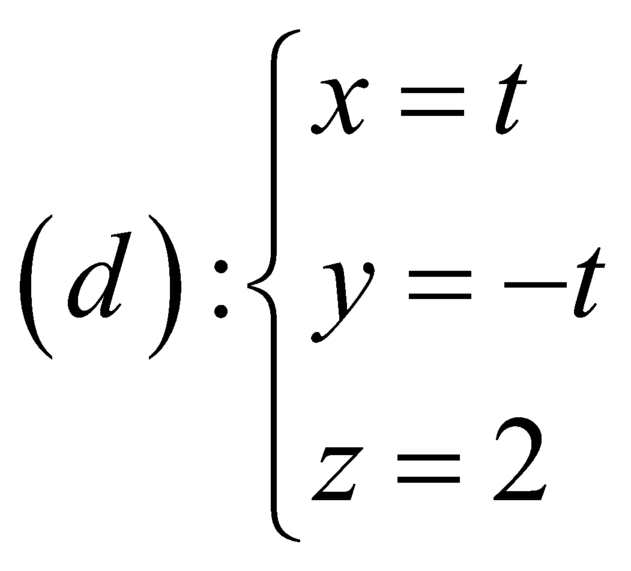
D. 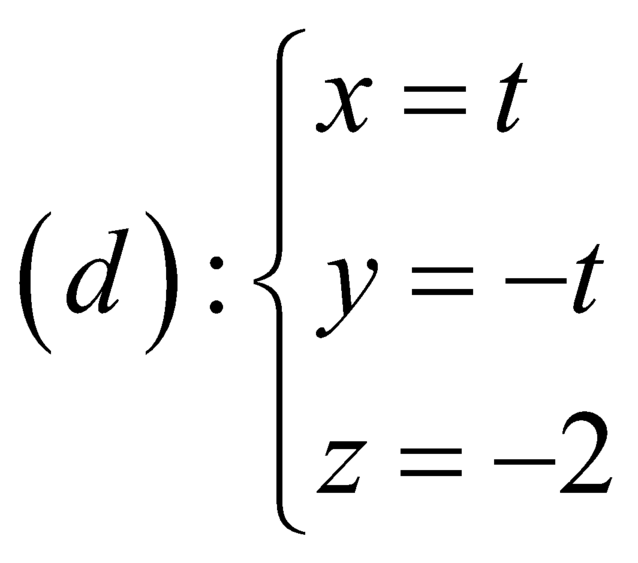 .
.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;0;2) ; N(1;-1;-1) và mặt phẳng (P): x + 2y - z + 2 0. Một mặt cầu đi qua M ; N tiếp xúc với mặt phẳng (P) tại điểm E . Biết E luôn thuộc một đường tròn cố định, tính bán kính đường tròn đó.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;0;2) ; N(1;-1;-1) và mặt phẳng (P): x + 2y - z + 2 = 0. Một mặt cầu đi qua M ; N tiếp xúc với mặt phẳng (P) tại điểm E . Biết E luôn thuộc một đường tròn cố định, tính bán kính đường tròn đó.
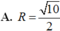
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²9 và đường thẳng
∆
:
x
-
6
-
3
y
-
2
2
z
-
2
2
. Phương trình mặt phẳng (P) đi qua điểm M (4;3;4) so...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 và đường thẳng ∆ : x - 6 - 3 = y - 2 2 = z - 2 2 . Phương trình mặt phẳng (P) đi qua điểm M (4;3;4) song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) là:
A.x-2y+2z-1=0.
B.2x+2y+z-18=0.
C.2x-y-2z-10=0.
D.2x+y+2z-19=0.
Trong không gian Oxyz, cho mặt cầu (S):
x
-
1
2
+
y
-
1
2
+
z
-
1
2
12
và mặt phẳng (P): x-2y+2z+110. Xét điểm M di động trên (P); các điểm A, B...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y - 1 2 + z - 1 2 = 12 và mặt phẳng (P): x-2y+2z+11=0. Xét điểm M di động trên (P); các điểm A, B, C phân biệt di động trên (S) sao cho AM, BM, CM là các tiếp tuyến của (S). Mặt phẳng (ABC) luôn đi qua điểm cố định nào dưới đây?
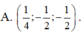
![]()
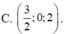
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
(
x
+
1
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
2
và...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 2 và hai đường thẳng d: x - 2 1 = y 2 = z - 1 - 1 , ∆ : x 1 = y 1 = z - 1 - 1 . Phương trình nào dưới đây là phương trình của một mặt phẳng tiếp xúc với (S), song song với d và ∆ ?
A. x+z+1=0
B. x+y+1=0
C. y+z+3=0
D. x+z-1=0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
1
y
+
2
1
z
1
và mặt phẳng (P): 2x+y-2z+20. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y + 2 1 = z 1 và mặt phẳng (P): 2x+y-2z+2=0. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1, phương trình mặt cầu (S) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
3
1
y
1
z
+
2
1
và điểm M (2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn? A. 2. B. 1 C. 0. D. Vô số.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 3 1 = y 1 = z + 2 1 và điểm M (2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn?
A. 2.
B. 1
C. 0.
D. Vô số.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-2y+z+30 và mặt cầu
S
:
x
−
1
2
+
y
+
3
2
+
z
2
9
và đường thẳng
d
:
x
−...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-2y+z+3=0 và mặt cầu S : x − 1 2 + y + 3 2 + z 2 = 9 và đường thẳng d : x − 2 = y + 2 1 = z + 1 2 . Cho các phát biểu sau đây:
I. Đường thẳng d cắt mặt cầu (S) tại 2 điểm phân biệt.
II. Mặt phẳng (P) tiếp xúc với mặt cầu (S)
III. Mặt phẳng (P) và mặt cầu (S) không có điểm chung
IV. Đường thẳng d cắt mặt phẳng (P) tại 1 điểm
Số phát biểu đúng là
A. 4
B. 1
C. 2
D. 3