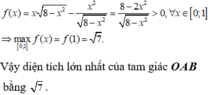Các câu hỏi tương tự
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
8
và điểm
M
1
2
;
3
2
;
0
Xét đường thẳng
△...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 = 8 và điểm M 1 2 ; 3 2 ; 0 Xét đường thẳng △ thay đổi qua điểm M, cắt (S) tại hai điểm phân biệt A, B. Diện tích lớn nhất của tam giác OAB bằng
A. 4
B. 7
C. 2 7
D. 8
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A (1;-1;2) và đường thẳng
d
:
x
1
y
2
z
+
2
-
2
. Mặt cầu (S) tâm A cắt đường thẳng d tại 2 điểm phân biệt B, C sao cho diện tích tam giác ABC bằng 12. Phương trình mặt cầu (S) là: A.
S
:...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A (1;-1;2) và đường thẳng d : x 1 = y 2 = z + 2 - 2 . Mặt cầu (S) tâm A cắt đường thẳng d tại 2 điểm phân biệt B, C sao cho diện tích tam giác ABC bằng 12. Phương trình mặt cầu (S) là:
A. S : x - 1 2 + y + 1 2 + z - 2 2 = 36
B. S : x - 1 2 + y + 1 2 + z - 2 2 = 25
C. S : x - 1 2 + y + 1 2 + z - 2 2 = 144
D. S : x - 1 2 + y + 1 2 + z - 2 2 = 64
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
−
1
3
y
+
2
−
1
z
+
1
2
;
d
2
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x − 1 3 = y + 2 − 1 = z + 1 2 ; d 2 : x = 3 t y = 4 − t z = 2 + 2 t và mặt phẳng Oxz cắt d 1 , d 2 lần lượt tại các điểm A, B. Diện tích S của tam giác OAB bằng bao nhiêu?
A. S = 5
B. S = 3
C. S = 6
D. S = 10
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
−
1
3
y
+
2
−
1
z
+
1
2
;
d
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x − 1 3 = y + 2 − 1 = z + 1 2 ; d 2 : x = 3 t y = 4 − t z = 2 + 2 t và mặt phẳng Oxz cắt d 1 , d 2 lần lượt tại các điểm A, B. Diện tích S của tam giác OAB bằng bao nhiêu?
A. S = 5.
B. S = 3.
C. S = 6.
D. S = 10.
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;0;2),B(0;2;-2). Các điểm M, N lần lượt di động trên các đoạn thẳng OA, OB sao cho MN chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi MN ngắn nhất thì toạ độ trọng tâm của tam giác OMN là A. (
2
4
;
2
4
; 0) B. (
2
3
;
2...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;0;2),B(0;2;-2). Các điểm M, N lần lượt di động trên các đoạn thẳng OA, OB sao cho MN chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi MN ngắn nhất thì toạ độ trọng tâm của tam giác OMN là
A. ( 2 4 ; 2 4 ; 0)
B. ( 2 3 ; 2 3 ; 0)
C. ( 1 3 ; 1 3 ; 0)
D. ( 1 4 ; 1 4 ; 0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
−
2
x
+
4
z
+
1
0
và đường thẳng
(
d
)
:
x
−
2
−...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x + 4 z + 1 = 0 và đường thẳng ( d ) : x − 2 − 1 = y 1 = z − m 1 . Tìm m để cắt tại hai điểm phân biệt A, B sao cho các tiếp diện của tại A và B vuông góc với nhau.
A. m = 1 hoặc m = 4
B. m = –1 hoặc m = –4.
C. m = 0 hoặc m = –1.
D. m = 0 hoặc m = –4.
Trong không gian Oxyz, cho mặt cầu (S) tâm I(−1;0;2) đi qua điểm A(0;1;1). Xét các điểm B, C, D thuộc (S) sao cho tam giác BCD vuông cân tại B, AB AC AD. Thể tích tứ diện ABCD có giá trị lớn nhất bằng A.
8
3
B.
16
3
27
C.
32...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) tâm I(−1;0;2) đi qua điểm A(0;1;1). Xét các điểm B, C, D thuộc (S) sao cho tam giác BCD vuông cân tại B, AB = AC = AD. Thể tích tứ diện ABCD có giá trị lớn nhất bằng
A. 8 3
B. 16 3 27
C. 32 3 27
D. 4 3
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(0;1;0), B(2,-1,2). Phương trình mặt phẳng (P) đi qua các điểm A, B và cắt tia Ox, Oz lần lượt tại M và N sao cho diện tích tam giác AMN nhỏ nhất. Điểm nào sau đây thuộc mặt phẳng (P). A. (1;3;2) B. (1;3;-2) C. (2;3;-2) D. (2;3;-6)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(0;1;0), B(2,-1,2). Phương trình mặt phẳng (P) đi qua các điểm A, B và cắt tia Ox, Oz lần lượt tại M và N sao cho diện tích tam giác AMN nhỏ nhất. Điểm nào sau đây thuộc mặt phẳng (P).
A. (1;3;2)
B. (1;3;-2)
C. (2;3;-2)
D. (2;3;-6)
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng
P
:
x
+
y
-
z
+
2
0
và hai điểm
A
7
;
-
4
;
-
3
,
B
3
;
4
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng P : x + y - z + 2 = 0 và hai điểm A 7 ; - 4 ; - 3 , B 3 ; 4 ; 1 . Gọi M a ; b ; c là điểm thuộc P a < 2 sao cho tam giác AMB vuông tại M và có diện tích nhỏ nhất. Giá trị của biểu thức 3 a + 9 b + 63 c bằng
A. 140
B. -38
C. 154
D. -21