Đáp án C
Giả sử M(m;0;0), N(0;0;n) do M,N thuộc các tia Ox, Oz nên m,n >0.
Mặt phẳng (P) đi qua A,M,N có phương trình là
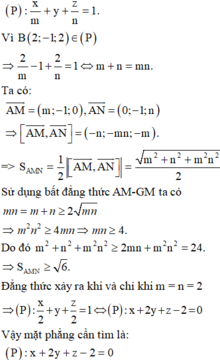
Đáp án C
Giả sử M(m;0;0), N(0;0;n) do M,N thuộc các tia Ox, Oz nên m,n >0.
Mặt phẳng (P) đi qua A,M,N có phương trình là
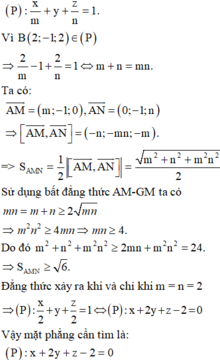
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M( 1; 2;3) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho T = 1 O A 2 + 1 O B 2 + 1 O C 2 đạt giá trị nhỏ nhất có dạng (P): x + ay + bz + c = 0 . Tính S = a + b + c
A. 19.
B. 6
C. -9.
D. -5.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;1;1). Viết phương trình mặt phẳng (P) đi qua M và cắt ba tia Ox, Oy, Oz lần lượt tại các điểm A, B, C khác gốc O sao cho thể tích khối tứ diện OABC nhỏ nhất.
A. 2x-y+2z-3=0
B. 4x-y-z-6=0
C. 2x+y+2z-6=0
D. x+2y+2z-6=0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M 1 ; 2 ; 3 và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 6 x + 3 y − 2 z − 6 = 0
B. x + 2 y + 3 z − 14 = 0
C. x + 2 y + 3 z − 11 = 0
D. x 1 + y 2 + z 3 = 3
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3 x + 2 y + z + 14 = 0
B. 2 x + y + 3 z + 9 = 0
C. 3 x + 2 y + z - 14 = 0
D. 2 x + y + z - 9 = 0
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B. C khác với gốc tọa độ sao cho biểu thức 6OA+3OB+2OC có giá trị nhỏ nhất
A. 6x+3y+2z-18=0
B. x+2y+3z-14=0
C. x+3y+2z-13=0
D. 6x+2y+3z-19=0
Trong không gian với hệ trục tọa độ Oxyz. Mặt phẳng (P) đi qua điểm M(1;27;8) cắt các tia Ox,Oy, Oz lần lượt tại A, B, C sao cho A B 2 + B C 2 + C A 2 nhỏ nhất có phương trình là
A. 6 x + 2 y + 3 z − 84 = 0.
B. 6 x − 2 y + 3 z + 24 = 0.
C. 6 x − 2 y − 3 z + 72 = 0.
D. 6 x + 2 y − 3 z − 36 = 0.
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các tia Ox;Oy;Oz lần lượt tại các điểm A, B, C khác gốc tọa độ O sao cho biểu thức 6OA+3OB+2OC có giá trị nhỏ nhất.
A.6x+2y+3z-19 = 0
B. x+2y+3z-14 = 0
C. x+3y+2z-18 = 0
D. x+3y+2z-13 = 0
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (α) đi qua M(2;1;2) đồng thời cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho tứ diện OABC có thể tích nhỏ nhất. Phương trình mặt phẳng (α) là.
A. x+2y+z-1=0
B. 2x+y-2z-1=0
C. 2x+y+z-7=0
D. x+2y+z-6=0
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho T = 1 O A 2 + 1 O B 2 + 1 O C 2 đạt giá trị nhỏ nhất có dạng (P): x+ay+bz+c=0. Tính S=a+b+c
A. -5
B. 6
C. 19
D. -9