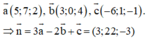Các câu hỏi tương tự
Trong không gian Oxyz, cho ba véc tơ
a
→
(
5
;
7
;
2
)
,
b
→
(
3
;
0
;
4
)
,
c
→
(
-
6
;
1
;
-
1
)
. Hãy tìm...
Đọc tiếp
Trong không gian Oxyz, cho ba véc tơ a → ( 5 ; 7 ; 2 ) , b → ( 3 ; 0 ; 4 ) , c → ( - 6 ; 1 ; - 1 ) . Hãy tìm véc tơ n → = 3 a → - 2 b → + c →
A. (3; 22; -3)
B. (-3; 22; 3)
C. (3; -22; 3)
D. (3; -22; -3)
Trong không gian Oxyz, cho 2 véc tơ
a
→
(
1
;
-
5
;
2
)
,
b
→
(
2
;
-
4
;
0
)
Tính tích vô hướng của 2 véc tơ
a
→
và
b
→
. A. ...
Đọc tiếp
Trong không gian Oxyz, cho 2 véc tơ a → ( 1 ; - 5 ; 2 ) , b → ( 2 ; - 4 ; 0 ) Tính tích vô hướng của 2 véc tơ a → và b → .
A. a → . b → = - 22
B. a → . b → = 22
C. a → . b → = 11
D. a → . b → = - 11
Trong không gian Oxyz, cho hai véc tơ
a
→
−
4
;
5
;
−
3
và
b
→
2
;
−
2
;
3
.
.Véc tơ
x
→
a...
Đọc tiếp
Trong không gian Oxyz, cho hai véc tơ a → = − 4 ; 5 ; − 3 và b → = 2 ; − 2 ; 3 .
.Véc tơ x → = a → + 2 b → có tọa độ là
A. − 2 ; 3 ; 0
B. 0 ; 1 ; − 1
C. 0 ; 1 ; 3
D. − 6 ; 8 ; − 3
Trong không gian với hệ tọa độ Oxyz cho hai véc tơ
a
→
3
;
0
;
2
,
c
→
1
;
−
1
;
0
.
Tìm tọa độ của véc tơ
b
→...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai véc tơ a → = 3 ; 0 ; 2 , c → = 1 ; − 1 ; 0 . Tìm tọa độ của véc tơ b → thỏa mãn biểu thức 2 b → − a → + 4 c → = 0 →
A. 1 2 ; − 2 ; − 1
B. − 1 2 ; 2 ; 1
C. − 1 2 ; − 2 ; 1
D. − 1 2 ; 2 ; − 1
Trong không gian Oxyz cho
a
→
1
;
2
;
1
,
b
→
−
1
;
1
;
2
,
c
→
x
;
3...
Đọc tiếp
Trong không gian Oxyz cho a → 1 ; 2 ; 1 , b → − 1 ; 1 ; 2 , c → x ; 3 x ; x + 2 . Nếu 3 véc tơ a → , b → , c → đồng phẳng thì x bằng
A. -1
B. 1
C. -2
D. 2
Trong không gian Oxyz, cho hai véc tơ
a
→
2
;
4
;
−
2
và
b
→
3
;
−
1
;
6
.
Tính
P
a
→
....
Đọc tiếp
Trong không gian Oxyz, cho hai véc tơ a → 2 ; 4 ; − 2 và b → 3 ; − 1 ; 6 . Tính P = a → . b → .
A. P = − 10.
B. P = − 40.
C. P = 16.
D. P = − 34.
Cho véc tơ
n
→
≠
0
→
và hai véc tơ không cùng phương
a
→
,
b
→
. Nếu véc tơ
n
→
vuông góc với
a
→
,
b
→
thì ba véc tơ
n
→
,
a...
Đọc tiếp
Cho véc tơ n → ≠ 0 → và hai véc tơ không cùng phương a → , b → . Nếu véc tơ n → vuông góc với a → , b → thì ba véc tơ n → , a → , b →
A. Đồng phẳng.
B. Có thể đồng phẳng.
C. Có thể không đồng phẳng.
D. Không đồng phẳng.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M( 1; -1; -2), N(3; 5; 7). Tính tọa độ của véc tơ
M
N
→
. A.
M
N
→
(
2
;
9
;
6
)
B.
M
N
→
(
2
;
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M( 1; -1; -2), N(3; 5; 7). Tính tọa độ của véc tơ M N → .
A. M N → = ( 2 ; 9 ; 6 )
B. M N → = ( 2 ; 6 ; 9 )
C. M N → = ( 6 ; 2 ; 9 )
D. M N → = ( 6 ; 2 ; - 9 )
Trong không gian với hệ trục Oxyz, cho 2 điểm
A
(
2
;
1
;
−
3
)
;
B
(
2
;
4
;
1
)
.
Gọi (d) là đường thẳng đi qua trọng tâm tam giác ABO sao cho tổng khoảng cách từ các điểm A, B, O đến đường thẳng (d) là lớn nhất. Trong các véc tơ sau, véc tơ nào là một véc tơ chỉ phương của (d)? A.
u
→...
Đọc tiếp
Trong không gian với hệ trục Oxyz, cho 2 điểm A ( 2 ; 1 ; − 3 ) ; B ( 2 ; 4 ; 1 ) . Gọi (d) là đường thẳng đi qua trọng tâm tam giác ABO sao cho tổng khoảng cách từ các điểm A, B, O đến đường thẳng (d) là lớn nhất. Trong các véc tơ sau, véc tơ nào là một véc tơ chỉ phương của (d)?
A. u → = 13 ; 8 ; 6
B. u → = − 13 ; 8 ; 6
C. u → = 13 ; 8 ; − 6
D. u → = − 13 ; 8 ; − 6