Phương trình mặt phẳng (ABC) là:
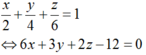
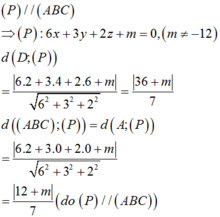
Theo đề bài, ta có:
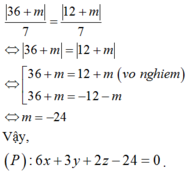
Chọn A.
Phương trình mặt phẳng (ABC) là:
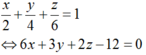
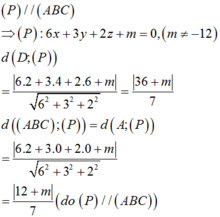
Theo đề bài, ta có:
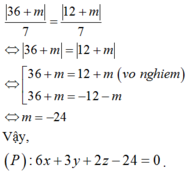
Chọn A.
Trong không gian với hệ tọa độ (Oxyz), cho đường thẳng d : x 1 = y - 1 2 = z + 1 1 và mặt phẳng (P): x + y + z - 2 = 0. Gọi d' là đường thẳng vuông góc d và song song với mp(P). Véctơ chỉ phương của d' là:
A. u → = 0 ; - 1 ; 1
B. u → = 1 ; 0 ; - 1
C. u → = 2 ; - 1 ; - 1
D. u → = 1 ; 1 ; - 2
Trong không gian Oxyz, cho điểm A(1; 2; -1), đường thẳng d có phương trình x - 3 1 = y - 3 3 = z 2
và mặt phẳng (a) có phương trình x + y - z + 3 = 0 . Đường thẳng D đi qua điểm A , cắt d và song song với mặt phẳng (a) có phương trình là
A. x - 1 1 = y - 2 - 2 = z + 1 - 1
B. x - 1 1 = y - 2 2 = z + 1 1
C. x - 1 1 = y - 2 2 = z - 1 1
D. x - 1 - 1 = y - 2 - 2 = z + 1 1
Trong không gian Oxyz, cho mặt phẳng ( P ) : x + y + z - 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z - 2 - 1 . Đường thẳng d’ đối xứng với d qua mặt phẳng (P) có phương trình là
A. x - 1 1 = y - 1 - 2 = z - 1 7
B. x - 1 1 = y - 1 2 = z + 1 - 7
C. x - 1 1 = y + 1 - 2 = z + 1 7
D. x + 1 - 1 = y - 1 2 = z - 1 - 7
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x+y+z-2=0, (Q): x+2y-z+3=0 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q) là:
A. d : x - 1 - 3 = y 2 = z - 4 1
B. d : x - 1 3 = y 1 = z - 4 1
C. d : x - 1 - 3 = y - 1 = z - 4 1
D. d : x - 1 - 3 = y 2 = z - 4 - 1
Trong không gian Oxyz viết phương trình đường thẳng d song song với hai mặt phẳng (P): 3x+12y-3z-5=0, (Q): 3x-4y+9z+7=0 và đồng thời cắt cả hai đường thẳng d 1 : x + 5 2 = y - 3 - 4 = z + 1 3 ,
d 2 : x - 3 - 2 = y + 1 3 = z - 2 4
A. x + 3 8 = y + 1 3 = z - 2 4
B. x - 3 8 = y + 1 3 = z - 2 4
C. x + 3 - 8 = y + 1 3 = z + 2 4
D. x + 3 - 8 = y + 1 3 = z - 2 4
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P = x + y + z − 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z − 2 − 1 . Đường thẳng d ' đối xứng với d qua mặt phẳng (P) có phương trình là
A. x + 1 1 = y + 1 2 = z + 1 7
B. x + 1 1 = y + 1 − 2 = z + 1 7
C. x − 1 1 = y − 1 2 = z − 1 7
D. x − 1 1 = y − 1 − 2 = z − 1 7
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng ∆ là giao tuyến của hai mặt phẳng P : z - 1 = 0 và Q : x + y + z - 3 = 0 . Gọi d là đường thẳng nằm trong mặt phẳng P , cắt đường thẳng x - 1 1 = y - 2 - 1 = z - 3 - 1 và vuông góc với đường thẳng . Phương trình của đường thẳng d là
A. x = 3 + t y = t z = 1 + t
B. x = 3 - t y = t z = 1
C. x = 3 + t y = t z = 1
D. x = 3 + t y = - t z = 1 + t
Trong không gian Oxyz, cho mặt phẳng α : 2 x + y - 2 z - 2 = 0 , đường thẳng d : x + 1 2 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng α , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 2
B. 21 2
C. 7 3
D. 3 2
Trong không gian Oxyz, cho hai điểm A ( 0 ; 1 ; 1 ) , B ( 1 ; 0 ; 0 ) và mặt phẳng ( P ) : x + y + z - 3 = 0 . Gọi (Q) là mặt phẳng song song với (P) đồng thời đường thẳng AB cắt (Q) tại C sao cho CA = 2 CB . Mặt phẳng (Q) có phương trình là:
A . ( Q ) : x + y + z - 4 3 = 0
B . ( Q ) : x + y + z = 0 hoặc ( Q ) : x + y + z - 2 = 0
C . ( Q ) : x + y + z = 0
D . ( Q ) : x + y + z - 4 3 = 0 hoặc ( Q ) : x + y + z = 0