Ta có 
Vậy điều kiện tam giác OMN vuông cân là OM = ON > 0.
Gọi M(a;b;0), N(0;0;c)(c#0)
![]()
Do ba điểm A, M, N thẳng hàng nên A M ⇀ = k A N ⇀
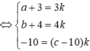
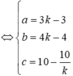
Suy ra  (k#1,k#0)
(k#1,k#0)
Có ![]()
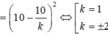
Đối chiếu điều kiện nhận k = ± 2
Vậy có hai đường thẳng thoả mãn.
Chọn đáp án C.
Ta có 
Vậy điều kiện tam giác OMN vuông cân là OM = ON > 0.
Gọi M(a;b;0), N(0;0;c)(c#0)
![]()
Do ba điểm A, M, N thẳng hàng nên A M ⇀ = k A N ⇀
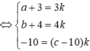
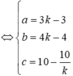
Suy ra  (k#1,k#0)
(k#1,k#0)
Có ![]()
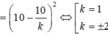
Đối chiếu điều kiện nhận k = ± 2
Vậy có hai đường thẳng thoả mãn.
Chọn đáp án C.
Trong không gian Oxyz, có bao nhiêu đường thẳng đi qua điểm và cắt trục tọa độ Oz tại điểm N, cắt mặt phẳng tọa độ tại điểm M sao cho tam giác OMN vuông cân
A. Hai.
B. Vô số.
C. Ba.
D. Một
Trong không gian tọa độ Oxyz, cho điểm M(2;-1;0). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho O A = 2 O B = 3 O C ≠ 0 ?
A. 4
B. 3
C. 2
D. 8
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;0). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho O A = 2 O B = 3 O C ≠ 0 ?
A. 4.
B. 3.
C. 2.
D. 8.
Trong không gian Oxyz, cho hai điểm M 1 ; 2 ; 3 , A 2 ; 4 ; 4 và hai mặt phẳng Q : x - 2 y - z + 4 = 0 , P : x + y - 2 z + 1 = 0 . Đường thẳng ∆ đi qua điểm M, cắt hai mặt phẳng P , Q lần lượt tại B và C a ; b ; c sao cho tam giác ABC cân tại A và nhận AM làm đường trung tuyến. Tính T = a + b + c .
A. T = 9
B. T = 3
C. T = 7
D. T = 5
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2) Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x Ox, y Oy, z Oz lần lượt tại các điểm A, B, C sao cho O A = O B = O C ≠ 0 ?
A. 3
B. 1
C. 4
D. 8
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C. Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. x 1 + y 2 + z 3 = 3
B. 6 x + 3 y − 2 z − 6 = 0
C. x + 2 y + 3 z − 14 = 0
D. x + 2 y + 3 z − 11 = 0
Trong không gian với hệ toạ độ Oxyz, cho điểm M(4;3;2). Có bao nhiêu mặt phẳng qua M cắt ba trục toạ độ Ox,Oy,Oz lần lượt tại A,B,C sao cho 6OA=2OB=3OC>0.
A. 8.
B. 1.
C. 3.
D. 4.
Trong không gian Oxyz cho điểm M(2;1;5) Mặt phẳng (P) đi qua điểm M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho M là trực tâm của tam giác ABC. Tính khoảng cách từ điểm I(1;2;3) đến mặt phẳng (P)
A. 17 30 30
B. 13 30 30
C. 19 30 30
D. 11 30 30
Trong không gian Oxyz cho điểm A (1;2;-3) và mặt phẳng (P): 2x + 2y - z + 9 = 0 Đường thẳng d đi qua A vuông góc với mặt phẳng (Q): 3x + 4y - 4z + 1 = 0 và cắt mặt phẳng (P) tại điểm B. Điểm M nằm trong (P) sao cho M luôn nhìn AB dưới góc vuông. Tính độ dài lớn nhất của MB
A. 41 2
B. 5 2
C. 5
D. 41