Các câu hỏi tương tự
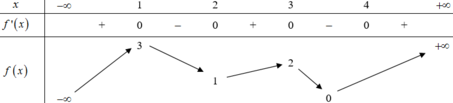
Cho hàm số f(x) có bảng biến thiên như sau:Hàm số
y
(
f
(
x
)
)
3
-
3
(
f
(
x
)
)
2
nghịch biến trên khoảng nào dưới đây? A. (2;3). B. (1;2). C. (3;4). D. (-∞;1).
Đọc tiếp
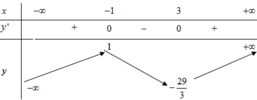
Cho hàm số f(x) có bảng biến thiên như sau:
Hàm số y = ( f ( x ) ) 3 - 3 ( f ( x ) ) 2 nghịch biến trên khoảng nào dưới đây?
A. (2;3).
B. (1;2).
C. (3;4).
D. (-∞;1).
Hàm số y f(x) có đồ thị như hình bên là một trong bốn hàm được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A.
y
x
+
1
x
−
2
.
B.
y
x
4
−
4
x
2
+
2.
C.
y...
Đọc tiếp
Hàm số y = f(x) có đồ thị như hình bên là một trong bốn hàm được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = x + 1 x − 2 .
B. y = x 4 − 4 x 2 + 2.
C. y = x 3 − 3 x 2 + 2.
D. y = x 3 + x 2 + 2.
Hàm số y f(x) có đồ thị như hình bên là một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào A.
f
x
x
3
−
3
x
2
.
B.
f
x
−
x
3
+
3
x
....
Đọc tiếp
Hàm số y = f(x) có đồ thị như hình bên là một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào
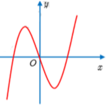
A. f x = x 3 − 3 x 2 .
B. f x = − x 3 + 3 x .
C. f x = x 4 − 2 x 2 .
D. f x = x 3 − 3 x .
Hàm số y f(x) có đồ thị như hình bên là một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A.
f
(
x
)
x
3
−
3
x
2
B.
f
(
x
)
−
x
3
+
3
x
C.
f
(
x
)...
Đọc tiếp
Hàm số y = f(x) có đồ thị như hình bên là một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
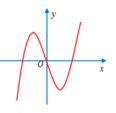
A. f ( x ) = x 3 − 3 x 2
B. f ( x ) = − x 3 + 3 x
C. f ( x ) = x 4 − 2 x 2
D. f ( x ) = x 3 − 3 x
Cho bài toán: “Xét tính đơn điệu của hàm số
y
x
2
+
2
x
-
3
” Một bạn học sinh đã làm bài như sau:Bước 1: Tập xác định:
D
ℝ
(
-
3
;
1
)
Bước 2: Tìm đạo hàm:
y
x
2...
Đọc tiếp
Cho bài toán: “Xét tính đơn điệu của hàm số y = x 2 + 2 x - 3 ” Một bạn học sinh đã làm bài như sau:
Bước 1: Tập xác định: D = ℝ \ ( - 3 ; 1 )
Bước 2: Tìm đạo hàm: y ' = x 2 + 2 x - 3 ' 2 x 2 + 2 x - 3 = x + 1 x 2 + 2 x - 3
Bước 3: y ' = 0 ⇔ x + 1 = 0 x 2 + 2 x - 3 > 0 ⇔ x = 1 x < - 3 ⇔ x ∈ ∅ ; x > 1
Bước 4: Bảng biến thiên:
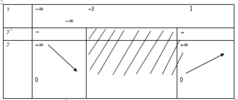
Bước 5: Kết luận:
Vậy hàm số nghịch biến trên nửa khoảng ( - ∞ ; - 3 ] , đồng biến trên nửa khoảng [ 1 ; + ∞ ) . Hỏi bài làm trên đúng hay
sai? Nếu sai thì sai từ bước nào?
A. Bài làm đúng.
B. Sai từ bước 3.
C. Sai từ bước 4.
D. Sai từ bước 5
Cho hàm số f(x) có
f
(
2
)
f
(
-
2
)
0
và có bảng xét dấu của đạo hàm như sau:Hàm số
y
(
f
(
3
-
x
)
)
2
nghịch biến trên khoảng nào dưới đây? A. (2;5). B. (1;+∞). C. (-2;-1). D. (1;2).
Đọc tiếp
Cho hàm số f(x) có f ( 2 ) = f ( - 2 ) = 0 và có bảng xét dấu của đạo hàm như sau:

Hàm số y = ( f ( 3 - x ) ) 2 nghịch biến trên khoảng nào dưới đây?
A. (2;5).
B. (1;+∞).
C. (-2;-1).
D. (1;2).
Cho hàm số yf(x) có đạo hàm f(x)
x
(
x
-
1
)
2
(
x
2
+
m
x
+
9
)
. Có bao nhiêu số nguyên dương m để hàm số yf(3-x) đồng biến trên khoảng
(
3
;
+
∞
)
. A. 6. B. 8. C. 5. D. 7.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Cho hàm số y f (x) có bảng biến thiên như sauSố nghiệm thực của phương trình 2 f (x) + 3 0 là A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Cho hàm số y = f (x) có bảng biến thiên như sau
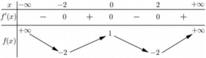
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là
A. 4
B. 3
C. 2
D. 1
Cho hàm số
y
f
x
x
3
−
x
+
1
và bốn hình vẽ lần lượt là 1, 2, 3, 4 dưới đây. Đồ thị của hàm số y f(x) là A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Đọc tiếp
Cho hàm số y = f x = x 3 − x + 1 và bốn hình vẽ lần lượt là 1, 2, 3, 4 dưới đây.
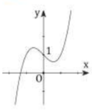
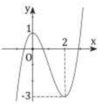
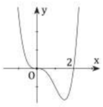
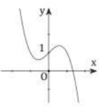
Đồ thị của hàm số y = f(x) là
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4