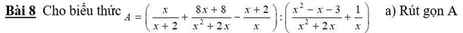a) \(A=5x^2-2x+1=5\left(x^2-\dfrac{2}{5}x+\dfrac{1}{25}\right)+\dfrac{4}{5}\)
\(=5\left(x-\dfrac{1}{5}\right)^2+\dfrac{4}{5}\ge\dfrac{4}{5}\)
\(minA=\dfrac{4}{5}\Leftrightarrow x=\dfrac{1}{5}\)
b) \(B=2x^2+4y^2+12x-4y-5=2\left(x^2-6x+9\right)+\left(4y^2-4y+1\right)-15\)
\(=2\left(x-3\right)^2+\left(2y-1\right)^2-15\ge-15\)
\(minB=-15\Leftrightarrow\) \(\left\{{}\begin{matrix}x=3\\y=\dfrac{1}{2}\end{matrix}\right.\)
c) \(C=9x^2+3y^2+6xy-4y=\left(9x^2+6xy+y^2\right)+2\left(y^2-2y+1\right)-2\)
\(=\left(3x+y\right)^2+2\left(y-1\right)^2-2\ge-2\)
\(minC=-2\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=1\end{matrix}\right.\)