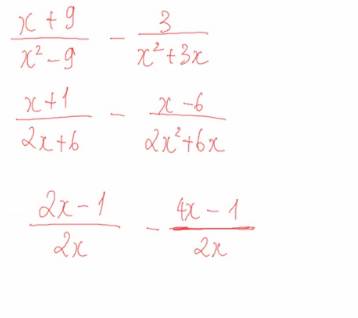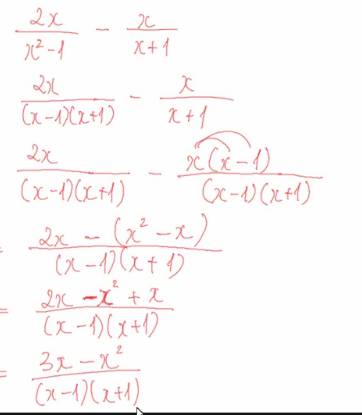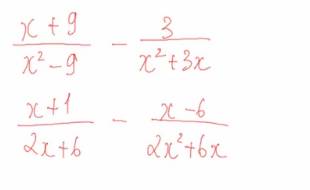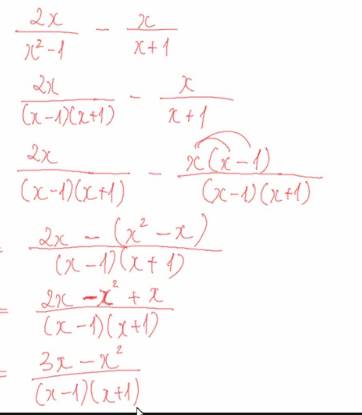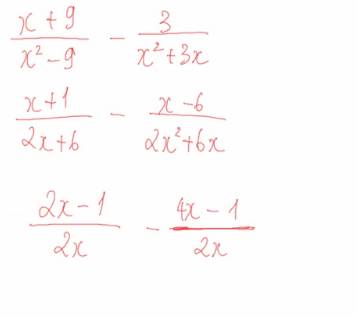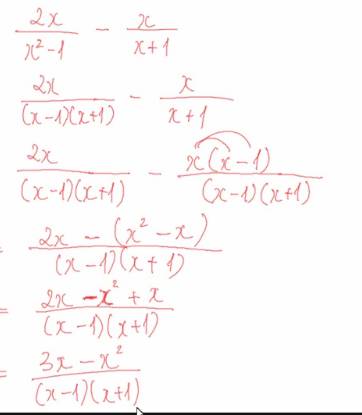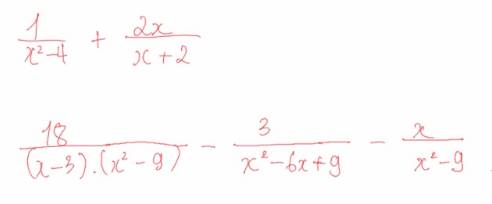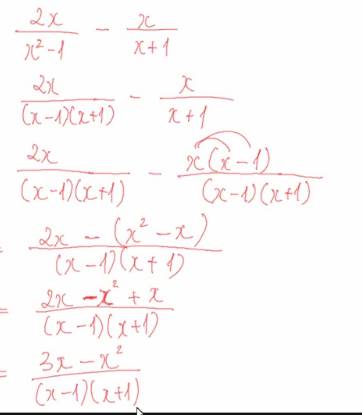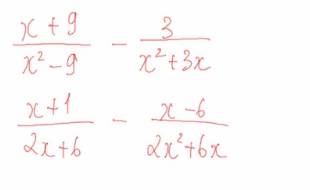Question

Mọi người ơi giúp mik voiwsii mai mik học rồi mà mik chx làm xong, cho mi câu trả lời chi tiết và rõ ràng nhất với ạ, xong thì mik sẽ tick

Đây là cách trình bày :

Answer 1

\(\dfrac{x+9}{x^2-9}-\dfrac{3}{x^2+3x}\)

= \(\dfrac{x+9}{\left(x-3\right).\left(x+3\right)}-\dfrac{3}{x.\left(x+3\right)}\)

=\(\dfrac{\left(x+9\right).x}{\left(x-3\right).\left(x+3\right).x}-\dfrac{3.\left(x-3\right)}{x.\left(x+3\right).\left(x-3\right)}\)

=\(\dfrac{x^2+9x}{x\left(x-3\right)\left(x+3\right)}-\dfrac{3x-9}{x\left(x-3\right)\left(x+3\right)}\)

=\(\dfrac{x^2+9-3x+9}{x\left(x-3\right)\left(x+3\right)}\)

=\(\dfrac{x^2-3x+18}{3\left(x-3\right)\left(x+3\right)}\)