Gọi pt BC có dạng: \(y=ax+b\Rightarrow\left\{{}\begin{matrix}0=6a+b\\3=a.0+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=3\\a=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow y=-\dfrac{1}{2}x+3\)
Pt hoành độ giao điểm BC và d:
\(-\dfrac{1}{2}x+3=mx-2m+2\)
\(\Leftrightarrow m\left(x-2\right)+\dfrac{1}{2}\left(x-2\right)=0\)
\(\Leftrightarrow\left(m+\dfrac{1}{2}\right)\left(x-2\right)=0\Rightarrow x=2\Rightarrow y=2\)
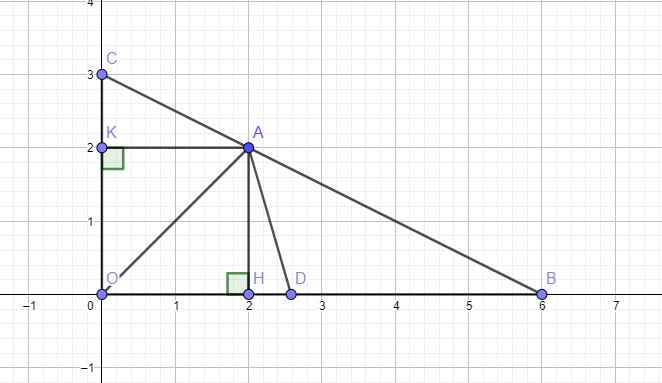
Vậy \(d_m\) luôn cắt BC tại điểm A cố định có tọa độ \(A\left(2;2\right)\)
b. Ta có: \(OB=\left|x_B\right|=6;OC=\left|y_C\right|=3\)
Từ A kẻ AH vuông góc trục hoành và AK vuông góc trục tung
\(\Rightarrow AH=\left|y_A\right|=2\) ; \(AK=\left|x_A\right|=2\)
\(S_{OAC}=\dfrac{1}{2}AK.OC=\dfrac{1}{2}.2.3=3\) ; \(S_{OAB}=\dfrac{1}{2}AH.OB=6\)
\(S_{OBC}=\dfrac{1}{2}OB.OC=9\)
Giả sử \(d_m\) cắt cạnh OC tại 1 điểm D nằm giữa O và C
\(\Rightarrow S_{ACD}=S_{OAC}-S_{OAD}< S_{OAC}=3< \dfrac{1}{2}S_{OBC}=9\) (ktm)
\(\Rightarrow d_m\) phải cắt cạnh OB tại 1 điểm D nào đó nằm giữa O và B
Khi đó: \(S_{ABD}=\dfrac{1}{2}S_{OBC}=\dfrac{9}{2}\)
Mà \(S_{ABD}=\dfrac{1}{2}AH.BD\Rightarrow BD=\dfrac{2S_{ABD}}{AH}=\dfrac{9}{2}\)
\(\Rightarrow x_B-x_D=\dfrac{9}{2}\Rightarrow x_D=6-\dfrac{9}{2}=\dfrac{3}{2}\)
\(\Rightarrow D\left(\dfrac{3}{2};0\right)\)
Do \(d_m\) qua D nên: \(\dfrac{3}{2}m-2m+2=0\Rightarrow m=4\)