Bài 1:
Gọi số cây trong của lớp 6A,6B lần lượt là a,b(cây)(a,b∈N*)
Ta có: \(\dfrac{a}{b}=0,875\Rightarrow\dfrac{a}{7}=\dfrac{b}{8}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{7}=\dfrac{b}{8}=\dfrac{b-a}{8-7}=\dfrac{23}{1}=23\)
\(\Rightarrow\left\{{}\begin{matrix}a=23.7=161\\b=23.8=184\end{matrix}\right.\)
Vậy....
Bài 2:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\\dfrac{y}{4}=\dfrac{z}{5}\end{matrix}\right.\)\(\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{20}{5}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=4.8=32\\y=4.12=48\\z=4.15=60\end{matrix}\right.\)
Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{20}{5}=4\)
Do đó: x=32; y=48; z=60
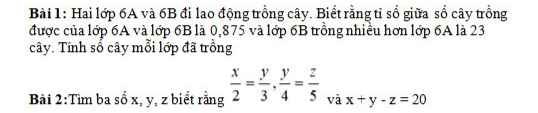
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
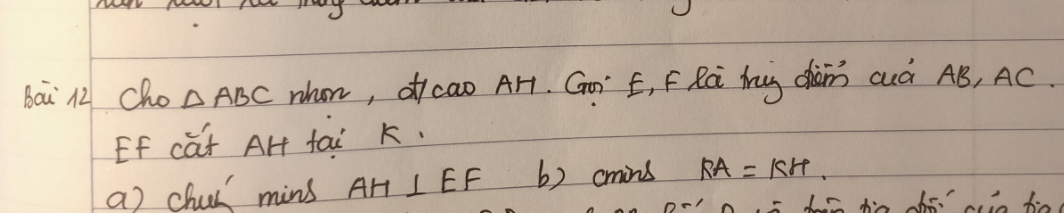
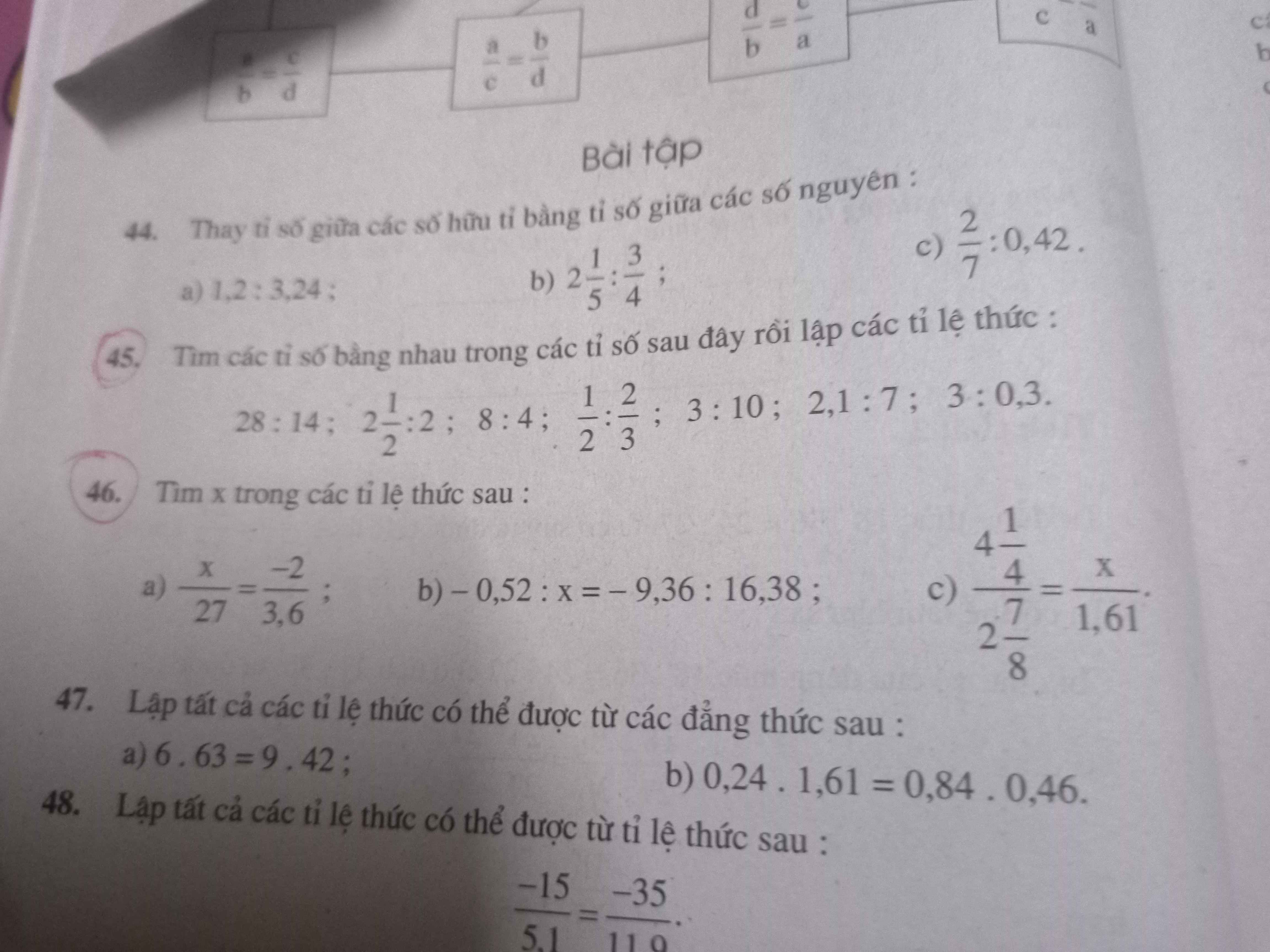
ai cứu em với ạ em cần nộp trc 7h10 ạ
