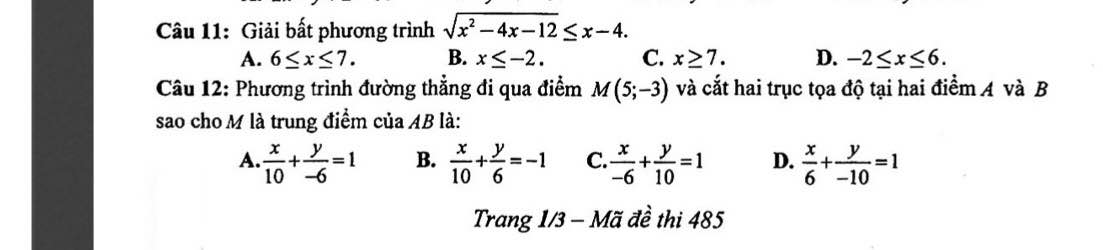a, Sai
Giải thích: \(sin\left(180^o-\alpha\right)=sin\alpha=\dfrac{5}{13}\)
b, Sai
Giải thích: \(90^o< \alpha< 180^o\Rightarrow cos\alpha< 0\)
c, Đúng
Giải thích:
Ta có:
\(sin^2\alpha+cos^2\alpha=1\)
\(\Rightarrow\left(\dfrac{5}{13}\right)^2+cos^2\alpha=1\)
\(\Rightarrow cos^2\alpha=\dfrac{144}{169}\) \(\Rightarrow cos\alpha=-\dfrac{12}{13}\left(do,cos\alpha< 0\right)\)
Ta có:
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=-\dfrac{5}{12};cot\alpha=\dfrac{cos\alpha}{sin\alpha}=\dfrac{-12}{5}\), thay vào biểu thức P ta có:
\(P=\dfrac{-\dfrac{5}{12}+2.\left(-\dfrac{12}{5}\right)}{-\dfrac{5}{12}-\left(-\dfrac{12}{5}\right)}=\dfrac{-313}{119}\)
d, Đúng
Giải thích:
\(E=sin^4x+sin^2x.cos^2x+cos^2x\)
\(E=\left(sinx^2\right)^2+sin^2x.cos^2x+cos^2x\)
\(E=sin^2x.\left(sin^2x+cos^2x\right)+cos^2x\)
\(E=sin^2x.1+cos^2x\) \(\left(do,sin^2x+cos^2x=1\right)\)
\(E=sin^2x+cos^2x=1\)
a: \(sin\left(180^0-\alpha\right)=sin\alpha=\dfrac{5}{13}\)
=>Sai
b: Vì \(\alpha>90^0\)
nên \(cos\alpha< 0\)
=>Sai
c:
Ta có: \(cos^2\alpha+sin^2\alpha=1\)
=>\(cos^2\alpha=1-\left(\dfrac{5}{13}\right)^2=1-\dfrac{25}{169}=\dfrac{144}{169}\)
mà \(cos\alpha< 0\)
nên \(cos\alpha=-\sqrt{\dfrac{144}{169}}=-\dfrac{12}{13}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{5}{13}:\dfrac{-12}{13}=-\dfrac{5}{12}\)
\(cot\alpha=1:tan\alpha=-\dfrac{12}{5}\)
\(P=\dfrac{tan\alpha+2\cdot cot\alpha}{tan\alpha-cot\alpha}\)
\(=\dfrac{-\dfrac{5}{12}+2\cdot\dfrac{-12}{5}}{-\dfrac{5}{12}-\dfrac{-12}{5}}=\dfrac{-\dfrac{5}{12}+\dfrac{-24}{5}}{\dfrac{-25}{60}+\dfrac{144}{60}}\)
\(=\dfrac{-25+\left(-288\right)}{60}:\dfrac{119}{60}=\dfrac{-313}{119}\)
=>Đúng
d: \(E=sin^4x+cos^2x+sin^2xcos^2x\)
\(=sin^2x\left(sin^2x+cos^2x\right)+cos^2x\)
\(=sin^2x+cos^2x=1\)
=>Đúng

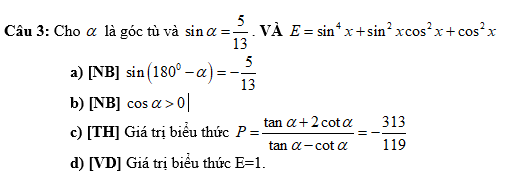











 Giải giúp mình phần trắc nghiệm với ạ
Giải giúp mình phần trắc nghiệm với ạ


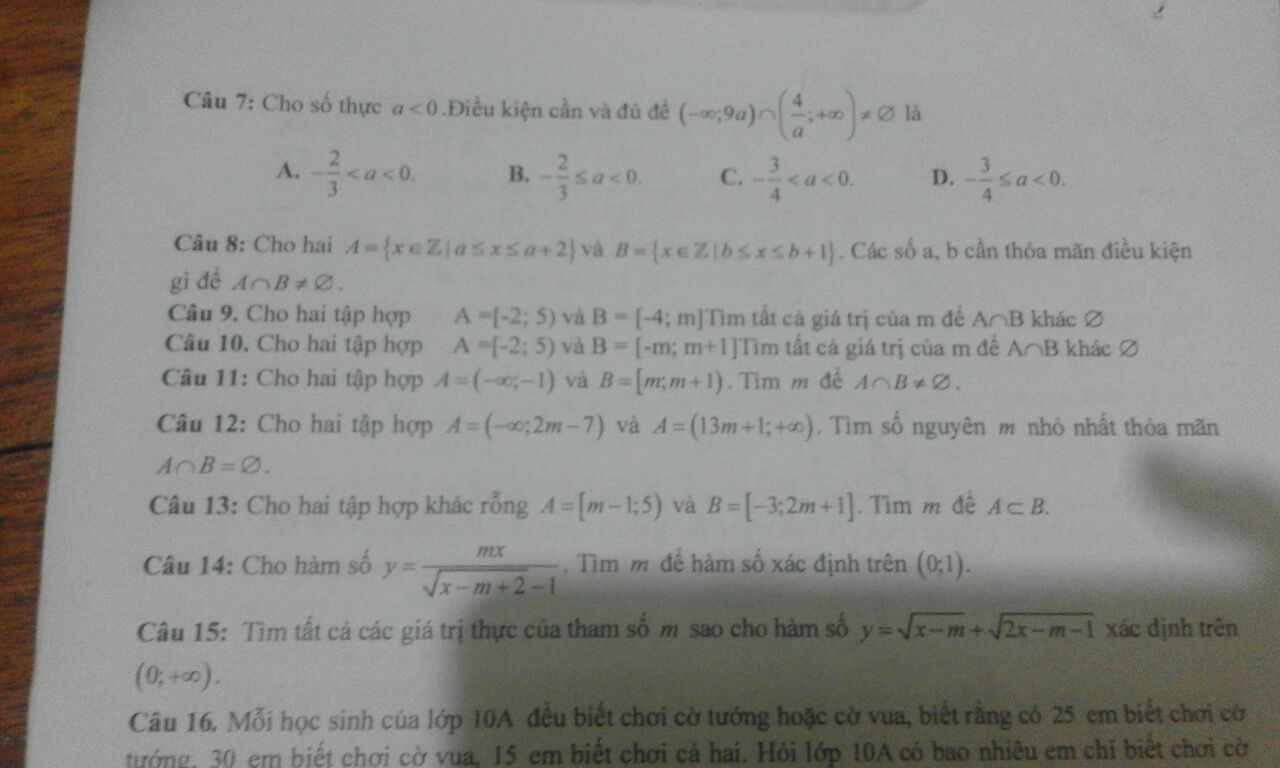 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!