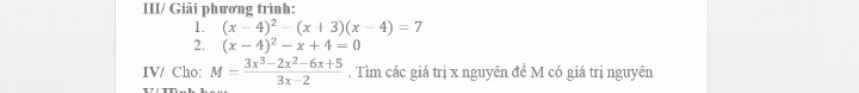\(a,=\dfrac{2y}{x}\\ b,=\dfrac{3\left(x+4\right)}{4\left(x-4\right)}\cdot\dfrac{-2\left(x-4\right)}{x+4}=\dfrac{-3}{2}\\ c,=\dfrac{\left(x+2\right)^2}{2\left(x-3\right)}\cdot\dfrac{x-3}{x+2}=\dfrac{x+2}{2}\\ d,=\dfrac{x+4+2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{3x}{x^2-4}\)
a, \(\dfrac{2y}{x}\)
b, \(\dfrac{3\left(x+4\right)}{4\left(x-4\right)}.\dfrac{-2\left(x-4\right)}{x+4}=\dfrac{-3}{2}\)
c, \(\dfrac{\left(x+2\right)^2}{2\left(x-3\right)}.\dfrac{x-3}{x+2}=\dfrac{x+2}{2}\)
d, \(\dfrac{x+4}{\left(x-2\right)\left(x+2\right)}+\dfrac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{x+4+2x-4}{\left(x+2\right)\left(x-2\right)}=\dfrac{3x}{x^2-4}\)
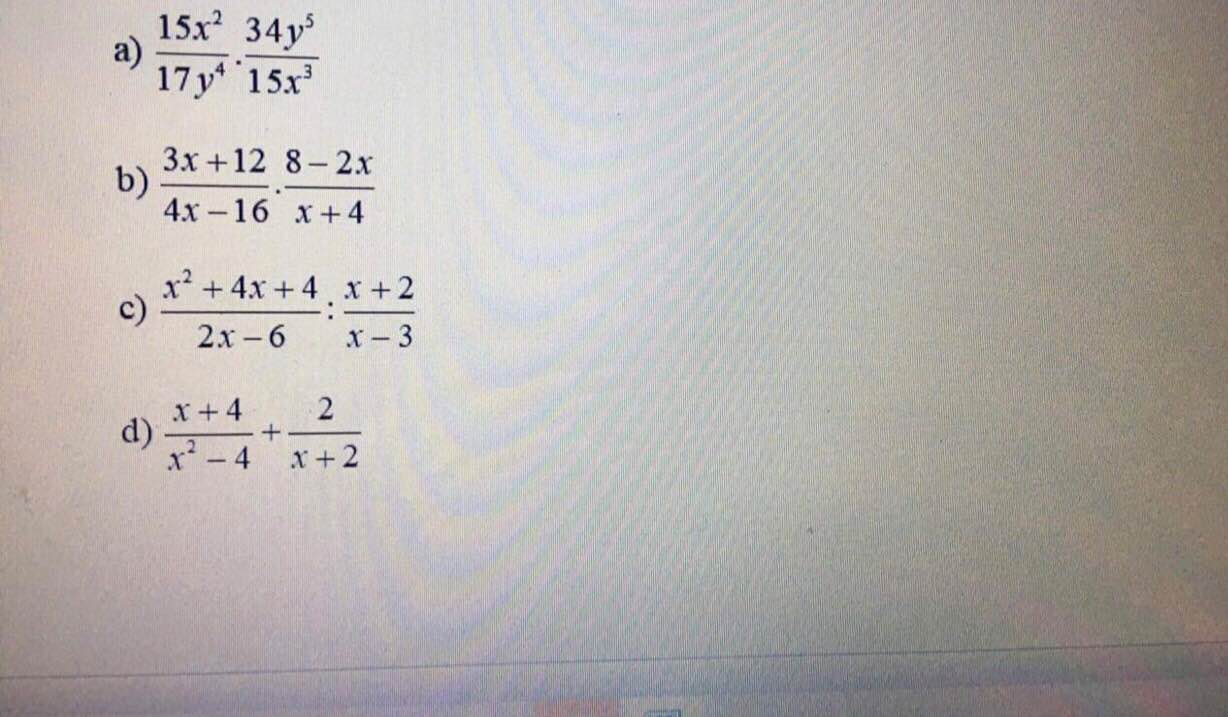
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
