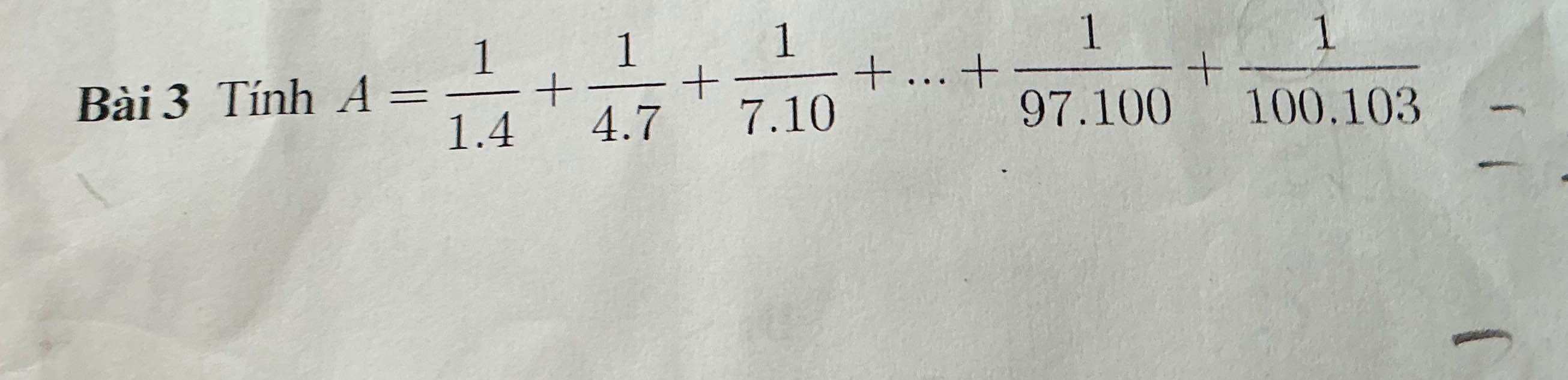\(\dfrac{1}{1\cdot4}+\dfrac{1}{4\cdot7}+\dfrac{1}{7\cdot10}+...+\dfrac{1}{97\cdot100}+\dfrac{1}{100\cdot103}\\ =\dfrac{1}{3}\cdot\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{97\cdot100}+\dfrac{3}{100\cdot103}\right)\\ =\dfrac{1}{3}\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}+\dfrac{1}{100}-\dfrac{1}{103}\right)\\ =\dfrac{1}{3}\cdot\left(1-\dfrac{1}{103}\right)\\ =\dfrac{1}{3}\cdot\dfrac{102}{103}\\ =\dfrac{34}{103}\)
`#3107.101107`
`3.`
`A = 1/(1*4) + 1/(4*7) + 1/(7*10) + ... + 1/(97*100) + 1/(100*103)`
`= 1/3 * (3/(1*4) + 3/(4*7) + 3/(7*10) + ... + 3/(97*100) + 3/(100*103))`
`= 1/3 * (1 - 1/4 + 1/4 - 1/7 + 1/7 - 1/10 + ... + 1/97 - 1/100 + 1/100 + 1/103)`
`= 1/3 * (1 - 1/103)`
`= 1/3 * 102/103 = 34/103`
Vậy, `A = 34/103.`