Chọn D
Đặt t = 4 - x 2 ⇒ d t = - 2 x d x ⇒ x d x = - d t 2
Khi x = 0 => t = 4; x = 2 => t = 0
D = ∫ 4 0 - 1 2 t d t = 1 2 ∫ 0 4 t 1 2 d t = 1 2 2 3 t 3 2 4 0 = 1 3 ( t t ) 4 0 = 1 3 ( 4 . 2 - 0 ) = 8 3
Chọn D
Đặt t = 4 - x 2 ⇒ d t = - 2 x d x ⇒ x d x = - d t 2
Khi x = 0 => t = 4; x = 2 => t = 0
D = ∫ 4 0 - 1 2 t d t = 1 2 ∫ 0 4 t 1 2 d t = 1 2 2 3 t 3 2 4 0 = 1 3 ( t t ) 4 0 = 1 3 ( 4 . 2 - 0 ) = 8 3
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
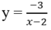
A. x = 2, y = 0 B. x = 0, y = 2
C. x = 1, x = 1 D. x = -2; y = -3
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
y = - 3 x - 2
A. x = 2, y = 0 B. x = 0, y = 2
C. x = 1, x = 1 D. x = -2; y = -3
Đường thẳng d:y=x-3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng △ : x - y = 0 Tính d=d1+d
A.![]()
B. ![]()
C. d = 6
D. ![]()
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c , d ∈ ℝ ) có đồ thị như hình vẽ bên
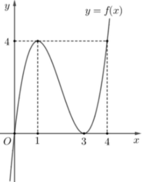
Phương trình f(f(f(f(x))) = 0 có tất cả bao nhiêu nghiệm thực phân biệt?
A. 12
B. 40
C. 41
D. 16
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Tính tổng tất cả các giá trị của m biết đồ thị hàm số y = x 3 - 2 mx 2 + ( m + 2 ) x + 4 và đường thẳng y = x + 4 cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng 8 2 với I(1;3)
A.3
B. 8
C. 1
D. 5
1.Tính các giá trị biểu thức sau:
a)510000.log52-59999.log52-...-53.log52-52.log52=?
b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43=?
2.Giải ptrình bậc cao sau:
a)x.(x2+y)150000-x.(x2+y)149999-...-x.(x2+y)2-x3-xy-2=0
b)xy(2y+1)50000-xy(2y+1)49999-...-xy(2y+1)2-2xy2-3=0
c)x2(x+1)10000-x2(x+1)9999-...-x2(x+1)2-x2(x+1)-x2-1=0
d)x.(\(\sqrt{x+1}\))10000-x.(\(\sqrt{x+1}\))9998-...-x.(\(\sqrt{x+1}\))4-x-3=0
3.Tính giá trị tại vị trí gián đoạn sau:
a)250000-249999-...-24-23=?Biết gián đoạn tại vị trí thứ 4
b)710000.log72-79999.log72-...-72.log72-7log72=?Biết gián đoạn tại vị trí 3->5
c)22+23+...+24999+25000=?Biết gián đoạn tại vị trí thứ 350 và vị trí 600
4.Thực hiện các yêu cầu sau:
Cho pt M: x.(x+1)50000-x.(x+1)49999-...-x.(x+1)3-x.(x+1)2-n=0
a.Xác định x=?
b.Tính n=?
c.Số nào dưới đây là số nguyên tố:
A.n+1/n-1
B.n+2/n-2
C.n+3/n-3
D.n+4/n-4
d.Xác định phương trình đồng dạng bậc 20(¶20)?
5.Cho ptrình bậc 2 sau:x2-2x=0
a.Xác định hàm P=?
A.P=(x2)x^2-2x B.P=(x2-2x)/(x2-2x) C.P=2xx^2 D.(x2-2x)x^2-2x
b.Xác định hàm P(x)?Biết Q(x)=2x+1
A.P(x)=2x B.P(x)=2.(x+1) C.P(x)=2.(x+2) D.P(x)=2.(x+3)
c.Tính lim(P/Q(x))=?
A.0 B.1 C.2 D.3
d.Ptrình bậc cao:250000-249999-...-22-21 ~ vs hàm nào cuả pt bậc 2?
A.2P=2.2xx^2-2x B.2P=2.x2.2x C.2P=2.22x D.2P=2.42x
e.Đồ thị hàm bậc cao nằm trên:
A.Trục tung B.Trục hoành C.A,B đúng D.A,C sai
f.Khi nào P=P(x)?
A.Q(x)=0 B.P(x)=0 C.P=0 D.Q(x)=P
g.Hãy biến ptrình bậc 3 sau về ptrình bậc cao:x3-x=0?
A.(x3-x)50000-(x3-x)49999-...-(x3-x)2-x3-x=0
B.(x3-x)50000-(x3-x)49999-...-(x3-x)2-x3+x=0
C.(x3+x)50000-(x3+x)49999-...-(x3+x)2-x3-x=0
D.(x3+x)50000-(x3+x)49999-...-(x3+x)2-x3+x=0
h.Từ ptrình bậc 3 ở câu g so sánh P1=xx^3-x và P2=x3.(x^3-x)
A.P1>P2 B.P1=P2 C.P1<P2 D.P1~P2
i.Từ câu h,hãy tính giá trị biểu thức sin(P1-1)+cos(P2-1)+tan(P1P2-P1-P2+1)=?
A.-3 B.-1 C.1 D.3
Giúp mik với