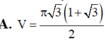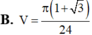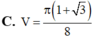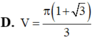Các câu hỏi tương tự
Cho lục giác đều ABCDEF có cạnh bằng 4. Quay lục giác đều đó quanh đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra A.
V
128
π
B.
V
32
π
C.
V
16
π
D.
V
64
π
Đọc tiếp
Cho lục giác đều ABCDEF có cạnh bằng 4. Quay lục giác đều đó quanh đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra
A. V = 128 π
B. V = 32 π
C. V = 16 π
D. V = 64 π
Cho lục giá đều ABCDEF có cạnh bằng 4. Cho lục giác đều đó quanh quay đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra. A.
V
128
π
B.
V
32
π
C.
V
16
π
D.
V
64
π
Đọc tiếp
Cho lục giá đều ABCDEF có cạnh bằng 4. Cho lục giác đều đó quanh quay đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra.
A. V = 128 π
B. V = 32 π
C. V = 16 π
D. V = 64 π
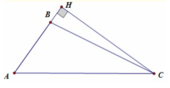
Cho tam giác ABC có AB3, BC5, CA7 Tính thể tích của khối tròn xoay sinh ra là do hình tam giác ABC quay quanh đường thẳng AB:
Đọc tiếp
Cho tam giác ABC có AB=3, BC=5, CA=7 Tính thể tích của khối tròn xoay sinh ra là do hình tam giác ABC quay quanh đường thẳng AB:
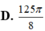
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8
π
Tính chiều cao của hình nón này.
Đọc tiếp
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8 π Tính chiều cao của hình nón này.
Cho tứ diện ABCD có AD
⊥
(ABC), ABC là tam giác vuông tại B. Biết BCA, ABa
3
, AD3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
Đọc tiếp
Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
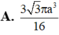
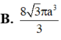
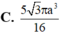
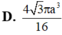
Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tam giác AGC quay quanh AG tạo thành một khối tròn xoay có thể tích là:
A
.
πa
3
3
36
B
.
πa
3
3
12
C
.
...
Đọc tiếp
Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tam giác AGC quay quanh AG tạo thành một khối tròn xoay có thể tích là:
A . πa 3 3 36
B . πa 3 3 12
C . πa 3 3 24
D . πa 3 3 18
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Cho đường tròn có bán kính bằng 4 và các nữa đường tròn có bán kính bằng 2 như hình vẽ. Khi quay hình tròn quanh cạnh AB thì các nửa đường tròn nhỏ sinh ra các khối tròn xoay có thể tích bằng bao nhiêu?
A. 71,6 π
B. 242,3 π
C. 62,5 π
Cho tam giác ABC có Quay tam giác ABC xung quanh cạnh BC ta đuợc khối tròn xoay có thể tích V bằng:
Đọc tiếp
Cho tam giác ABC có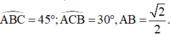 
Quay tam giác ABC xung quanh cạnh BC ta đuợc khối tròn xoay có thể tích V bằng:
