Ta có thể xem khối tròn xoay này là do hình giới hạn bởi bốn đường x = a, x = -a, y = b a a 2 - x 2 quay quanh trục Ox tạo nên.
Vậy
V = π ∫ a b b 2 a 2 a 2 - x 2 dx = πb 2 a 2 a 2 x - x 3 3 - a a = 4 a πab 2
Đáp án A
Ta có thể xem khối tròn xoay này là do hình giới hạn bởi bốn đường x = a, x = -a, y = b a a 2 - x 2 quay quanh trục Ox tạo nên.
Vậy
V = π ∫ a b b 2 a 2 a 2 - x 2 dx = πb 2 a 2 a 2 x - x 3 3 - a a = 4 a πab 2
Đáp án A
Cho hình phẳng D giới hạn bởi đường cong y = 3 + x − 2 e x x e x + 1 , trục hoành và hai đường thẳng x=0, x=1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V = π a + b ln 1 + 1 e , trong đó a, b là các số hữu tỷ. Mệnh đề nào dưới đây là đúng?
A. a+b=5
B. a-2b=5
C. a+b=3
D. a-2b=7
Cho hình phẳng (H) giới hạn bởi đường cong C : y = x 3 - 3 x + 2 và P : y = 2 x + 2 . Thể tích của khối tròn xoay nhận được khi cho (H) quay quanh trục Ox có dạng V = πa b + 2018 c + 2019 d . Hỏi mệnh đề nào trong các mệnh đề sau là sai?
A. abcd = 0
B. 9a - b - c - d = 1
C. a + b + 2 c + 3 d = 39
D. b + d a + c + 1 = 8
Thể tích khối vật thể tròn xoay khi quay hình phẳng (S) giới hạn bởi các đường y = 1 - x 2 , y = 0 quanh trục hoành có kết quả dạng π a b với a b là phân số tối giản. Khi đó a+b bằng:
A. 31
B. 23
C. 21
D. 32
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường y = 1 x − 3 , y = 0 , x = 0 , x = 2 quay một vòng quanh trục Ox là (theo đơn vị thể tích)
A. 2 π
B. 2 3 π
C. 4 3 π
D. 1 3 π
Thể tích khối tròn xoay khi quay xung quanh trục Ox hình phẳng giới hạn bởi đường cong y = 4 - x 2 , trục hoành và hai đường thẳng x=0;x=2 là
A. 32 3 π
B. π 2
C. 2 π 2
D. 16 3 π
Gọi H là hình phẳng giới hạn bởi P y = 3 x 2 , cung tròn y = 4 - x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Thể tích của khối tròn xoay thu được khi quay H xung quanh trục Ox bằng
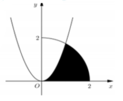
A. 34 15
B. 34 π 15
C. 43 15
D. 43 π 15
Cho hàm số y=f(x) liên tục trên đoạn a ; b và f(x)>0 ∀ x ∈ a ; b Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b (a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
A. ∫ a b f ( x 2 ) d x
B. π ∫ a b f ( x 2 ) d x
C. π ∫ a b [ f ( x ) ] 2 d x
D. ∫ a b [ f ( x ) ] 2 d x
Gọi V là thể tích khối tròn xoay thành thành khi quay hình phẳng giới hạn bởi các đường y = x , y = 0 và x = 4 quanh trục Ox. Đường thẳng x = a (0 < a < 4) cắt đồ thị hàm y = x tại M (hình vẽ bên). Gọi V 1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V = 2 V 1 . Khi đó:
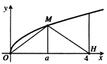
A. a = 2
B. a = 2 2
C. a = 5 2
D. a = 3
Thể tích vật thể tròn xoay sinh ra bởi hình elip x 2 a 2 + y 2 b 2 = 1 khi elip này quay xung quanh trục Ox là: .
A. 6
B. 13
C. 4 3 πab 2
D. 22