Ta có
3 . 9 x - 10 . 3 x + 3 = 0 ⇔ [ 3 x = 3 3 x = 1 3 ⇔ [ x = 1 x = - 1
Tích các nghiệm của phương trình đã cho là P=-1
Chọn đáp án B.
Ta có
3 . 9 x - 10 . 3 x + 3 = 0 ⇔ [ 3 x = 3 3 x = 1 3 ⇔ [ x = 1 x = - 1
Tích các nghiệm của phương trình đã cho là P=-1
Chọn đáp án B.
Tính P là tích tất cả các nghiệm của phương trình 3 . 9 x - 10 . 3 x + 3 = 0
A. P = 9
B. P = - 1
C. P = 1
D. P = 0
Tổng tất cả các nghiệm của phương trình 3 cos x - 1 = 0 trên đoạn 0 ; 4 π là :
A. 15 π 2
B. 6 π
C. 17 π 2
D. 8 π
Tập tất cả các giá trị của tham số m để phương trình m 1 + x + 1 - x + 3 + 2 1 - x 2 - 5 = 0 có đúng hai nghiệm thức phân biệt là một nửa khoảng (a;b] . Tính b - 5 7 a
A. 6 - 5 2 7
B. 6 - 5 2 35
C. 12 - 5 2 25
D. 12 - 5 2 7
Tập tất cả các giá trị của tham số thực m để phương trình m 1 + x + 1 - x + 3 + 2 1 - x 2 - 5 = 0 có đúng hai nghiệm phân biệt là một nửa khoảng (a;b]. Tính b - 5 7 a
A. 6 - 5 2 35
B. 6 - 5 2 7
C. 12 - 5 2 35
D. 12 - 5 2 7
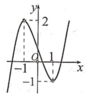
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Tất cả các giá trị của m để phương trình | f ( x ) | + m - 1 = 0 có 3 nghiệm phân biệt là
A. m=1
B. m=2
C. m = ± 1
D. m=0
Tất cả các nghiệm của phương trình tan x + 3 cot x − 3 − 1 = 0 là
A. x = π 4 + k π x = π 3 + k π k ∈ ℤ
B. x = − π 4 + k π x = π 6 + k π k ∈ ℤ
C. x = π 4 + k 2 π x = π 6 + k 2 π k ∈ ℤ
D. x = π 4 + k π x = π 6 + k π k ∈ ℤ
Tìm tất cả các nghiệm của phương trình tan x + 3 c o t x - 3 - 1 = 0 là
A. hoặc x = π 3 + k π , k ∈ Z
B. x = - π 4 + k π hoặc x = π 6 + k π , k ∈ Z
C. x = π 4 + k 2 π hoặc x = π 6 + k 2 π , k ∈ Z
D. x = π 4 + k π hoặc x = π 6 + k π , k ∈ Z
Cho phương trình 4 - x - a . log 3 x 2 - 2 x + 3 + 2 - x 2 + 2 x . log 1 3 2 x - a + 2 = 0 . Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm x 1 ; x 2 ; x 3 ; x 4 thỏa mãn là (c;d). Khi đó giá trị biểu thức T = 2 c + 2 d bằng:
A. 5
B. 2
C. 3
D. 4
Tích các nghiệm của phương trình 3 . 4 x + ( 3 x - 10 ) . 2 x + 3 - x = 0 là:
A. log 2 3
B. - log 2 3
C. 2 log 2 1 3
D. 2 log 2 3