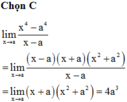Các câu hỏi tương tự
tính giới hạn
a) \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{2x+10}-4}{3x-9}\)
b) \(\lim\limits_{x\rightarrow7}\dfrac{\sqrt{4x+8}-6}{x^2-9x+14}\)
c) \(\lim\limits_{x\rightarrow5}\dfrac{x^2-8x+15}{2x^2-9x-5}\)
a) lim\(\dfrac{x^2-1}{x+1}\)(x-->-3)
b) lim\(\dfrac{4-x^2}{x+2}\)(x-->-2)
a) \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{2x+2}+\sqrt{5x+4}-5}{x-1}_{ }\)
b) \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4x+4}+\sqrt{90-6x}-5}{x^2}\)
4. Tính giới hạn \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x^2+1}-x-1}{2x^2-x}_{ }\)
5. Tính giới hạn:
a) \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{x^2-4}_{ }\)
b) \(\lim\limits_{x\rightarrow3^-}\dfrac{x+3}{x-3}_{ }\)
tính giới hạn
a) \(\lim\limits_{x\rightarrow4}\dfrac{\sqrt{2x+8}-4}{x-4}\)
b) \(\lim\limits_{x\rightarrow2}\dfrac{x^2-4}{\sqrt{4x+1}-3}\)
c) \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{2-\sqrt{x+2}}\)
\(a,\lim\limits_{x\rightarrow2}\dfrac{x^3+2x^2-6x-4}{8-x^3}\)
\(b,\lim\limits_{x\rightarrow2}\dfrac{x^3+x^2-5x-2}{x^2-3x+2}\)
Cho f(x) là hàm đa thức thỏa \(\lim\limits_{x\rightarrow2}\dfrac{f\left(x\right)+1}{x-2}=a\left(a\in R\right)\) và tồn tại \(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{f\left(x\right)+2x+1}-x}{x^2-4}=T\left(T\in R\right).\) Tìm T theo a.
Tính lim \(\left(x\rightarrow-\infty\right)\dfrac{\sqrt{x^4+4}}{x+4}\)
Câu 1: Tính giới hạn a, limdfrac{2-5^{n-2}}{3^n2.5^n} b,limdfrac{2-5^{n+2}}{3^n-2.5^n}Câu 2 :CMR :x^4+x^3-3x^2+x+10 có ít nhất một nghiệm âm lớn hơn -1Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Đọc tiếp
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
cho \(f\left(x\right)=\left\{{}\begin{matrix}x^2-3\\x+3\end{matrix}\right.\) \(x\ge3\);\(x< 3\)
a) tính \(\lim\limits_{x\rightarrow3^+}f\left(x\right)=?\)
\(\lim\limits_{x\rightarrow3^-}f\left(x\right)=?\)
b) tính \(\lim\limits_{x\rightarrow3}f\left(x\right)\) nếu có