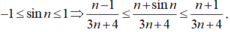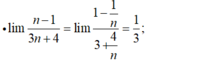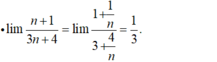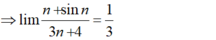Các câu hỏi tương tự
Bài 1: Phương trình căn 2 cot x + căn 2=0 có tổng các nghiệm khi k =0 và k=1?
A.3pi/4 B.5pi/4 C.4pi/3 D.pi/2Bài 2:cho sin a=1/3,0<a<pi/2 tính sin( a-pi/4) Bài 3:cho cos a=-2/3,pi/2<a<pi tính cos ( a+pi/3)
Giúp vs bạn
Câu 1: Tính giới hạn a, limdfrac{2-5^{n-2}}{3^n2.5^n} b,limdfrac{2-5^{n+2}}{3^n-2.5^n}Câu 2 :CMR :x^4+x^3-3x^2+x+10 có ít nhất một nghiệm âm lớn hơn -1Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Đọc tiếp
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, SD và BC. Gọi E là giao điểm của mặt phẳng (MNP) với cạnh SA. Tính tỉ số SE SA . A. 1 4 . B. 1 2 . C. 1 3 . D. 3
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4.2^{n+1}-3}{3.2^n+4^n}\right)\)
3) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{2-5^{n-2}}{3^n+2.5^n}\right)\)
1) Tính giới hạn \(K=\lim\limits_{n\rightarrow\infty}\left(\dfrac{3.2^n-3^n}{2^{n+1}+3^{n+1}}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n+1}{2^n-1}\right)\)
a) \(sinx=\dfrac{4}{3}\)
b) \(sin2x=-\dfrac{1}{2}\)
c) \(sin\left(x-\dfrac{\pi}{7}\right)\) = \(sin\dfrac{2\pi}{7}\)
d) \(2sin\left(x+\dfrac{\pi}{4}\right)=-\sqrt{3}\)
Cho hàm số
f
(
x
x
3
+
b
x
2
+
c
x
+
d
,
C
g
x
x
2
-
3
x
+
1
Với các số b, c, d tìm được ở bài 19, hãy:a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ...
Đọc tiếp
Cho hàm số f ( x = x 3 + b x 2 + c x + d , C g x = x 2 - 3 x + 1
Với các số b, c, d tìm được ở bài 19, hãy:
a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = - 1 .
b) Giải phương trình f ' sin x = 0 .
c) tính lim x → 0 f ' ' sin 5 x + 1 g ' sin 3 x + 3
Giải các pt: A, cos(4x + π/3)=✓3/2. ;. B, sin^2x-3sin3x+2=0. ;. C, tan(2x+10°)=√3. ;. D, tanx.cot2x=1
tính giới hạn \(\lim\limits_{n\rightarrow\infty}\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\)