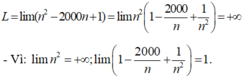Các câu hỏi tương tự
1. hàm số y = 3cosx luôn nhận giá trị trong tập nào
2. tập xác định của hàm số y = cosx
3. tính giới hạn \(L=\lim\limits\dfrac{n^2-3n^3}{2n^3+5n-2}\)
4. tính giới hạn \(L=\lim\limits\left(3n^2+5n-3\right)\)
5. kết quả của giới hạn \(\lim\limits_{n\rightarrow+\infty}\left(n^3-2n^2+3n-4\right)\)
1) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\sqrt{n^2-1}+3n\)
2) tính giới hạn I = \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{4n^2+5}+n\right)\)
Tính giới hạn L
l
i
m
n
3
-
2
n
3
n
2
+
n
-
2
A.
+
∞
B. 0 C.
1
3
D.
-
∞
Đọc tiếp
Tính giới hạn L= l i m n 3 - 2 n 3 n 2 + n - 2
A. + ∞
B. 0
C. 1 3
D. - ∞
Tính giới hạn
L
l
i
m
n
3
-
2
n
3
n
2
+
n
-
2
. A. L
+
∞
B. L 0 C. L
1...
Đọc tiếp
Tính giới hạn L = l i m n 3 - 2 n 3 n 2 + n - 2 .
A. L = + ∞
B. L = 0
C. L = 1 3
D. L = - ∞
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\dfrac{-n^2+2n+1}{\sqrt{3n^4+2}}\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{4n-\sqrt{16n^2+1}}{n+1}\right)\)
3) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{\sqrt{9n^2+n+1}-3n}{2n}\right)\)
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4.2^{n+1}-3}{3.2^n+4^n}\right)\)
3) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{2-5^{n-2}}{3^n+2.5^n}\right)\)
Tính giới hạn L=\(lim_{x\rightarrow0}\frac{\left(1+x\right)^n-1}{x}\).Với n là số nguyên dương
1) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{n^2+6n}-n\right)\)
2) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{n+1}-\sqrt{n-1}\right)\)
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n+1}{2^n-1}\right)\)
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{7^n+2^2}{3.7^n+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{1-4^n}{1+4^n}\right)\)