A = lim x → 2 2 x 2 − 5 x + 2 x 3 − 8 = lim x → 2 ( 2 x − 1 ) ( x − 2 ) ( x − 2 ) ( x 2 + 2 x + 4 ) = lim x → 2 2 x − 1 x 2 + 2 x + 4 = 1 4
Chọn đáp án C
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
tính giới hạn lim(x→0)\(\dfrac{ }{\dfrac{2\sqrt{2x+1}-\sqrt[3]{x^2+x+8}}{x}}\)
=\(\dfrac{a}{b}\)
tính a-2b=?
tính giới hạn
a) \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{2x+10}-4}{3x-9}\)
b) \(\lim\limits_{x\rightarrow7}\dfrac{\sqrt{4x+8}-6}{x^2-9x+14}\)
c) \(\lim\limits_{x\rightarrow5}\dfrac{x^2-8x+15}{2x^2-9x-5}\)
4. Tính giới hạn \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x^2+1}-x-1}{2x^2-x}_{ }\)
5. Tính giới hạn:
a) \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{x^2-4}_{ }\)
b) \(\lim\limits_{x\rightarrow3^-}\dfrac{x+3}{x-3}_{ }\)
Câu 1: Tính giới hạn a, limdfrac{2-5^{n-2}}{3^n2.5^n} b,limdfrac{2-5^{n+2}}{3^n-2.5^n}Câu 2 :CMR :x^4+x^3-3x^2+x+10 có ít nhất một nghiệm âm lớn hơn -1Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Đọc tiếp
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Tính các giới hạn sau:
a) $\underset{x\to 3}{\mathop{\lim }}\,\left( x+2 \right);$
b) $\underset{x\to +\infty }{\mathop{\lim }}\,\left( {{x}^{2}}-x+1 \right).$
Tìm a để hàm số
f
(
x
)
5
a
x
2
+
3
x
+
2
a
+
1
k...
Đọc tiếp
Tìm a để hàm số f ( x ) = 5 a x 2 + 3 x + 2 a + 1 k h i x ≥ 0 1 + x + x 2 + x + 2 k h i x < 0 có giới hạn tại x → 0
A. +∞
B. -∞
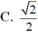
D. 1
giải phương trình
a) \(5^x=4\)
b) \(5^{2-x}=8\)
c) \(\left(\dfrac{1}{3}\right)^{4+x}=243\)
d) \(\left(\dfrac{2}{3}\right)^x=\dfrac{3}{2}\)
tính giới hạn
a) \(\lim\limits_{x\rightarrow4}\dfrac{\sqrt{2x+8}-4}{x-4}\)
b) \(\lim\limits_{x\rightarrow2}\dfrac{x^2-4}{\sqrt{4x+1}-3}\)
c) \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{2-\sqrt{x+2}}\)
Gọi `bb A` là giới hạn của hàm số `f(x)=[x+x^2+x^3+...+x^50 -50]/[x-1]` khi `x -> 1.` Tính giá trị của `bb A.`
tính giới hạn của hàm số
lim x->0 : \(\frac{\left(\sqrt{1+x^2}+x\right)^n-\left(\sqrt{1+x^2}-x\right)^n}{x^2}\)