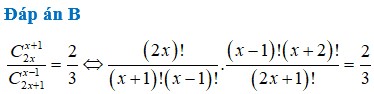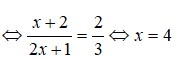Các câu hỏi tương tự
Tìm GTNN của các biểu thức sau:
a) \(A=!x-\frac{2}{7}!+0,5\)
b) \(B=!x-5!+!x-2!\)
c) \(C=!x-3!+!x+\frac{1}{2}!\)
Lưu ý: Dấu ! là giá trị tuyệt đối
câu 1 :Gía trị x=1 có phải là nghiệm của phương trình hya không?Vì sao?
câu 2:Tìm điều kiện xác định của mỗi phương trình sau:
a)\(\frac{x}{x-1}\)=\(\frac{x+4}{x+1}\)
b)\(\frac{3}{x-2}\)=\(\frac{2x+3}{x-2}\)
P(x) = -5x^4 + 2x^3 - 6x^2 + 3 - 5x
Q(x) = 5x^4 - 2x^3 + 6x^2 - 7 + x
a) Tính P(x) + Q(x)
b) Tìm nghiệm của đa thức P(x) + Q(x)
c) Tìm đa thức M(x) sao cho Q(x) + M(x) = -P(x)
d) Tìm một đa thức nhận số 0 và ( -1 ) làm nghiệm ? ![]()
Cho đa thức: Aleft(xright)2x^5-4x^3+x^2-2x+2 Bleft(xright)x^5-2x^4+x^2-5x+3 Cleft(xright)x^4+4x3+3x^2-8x+4frac{3}{16}a. Tính Mleft(xright)Aleft(xright)-2Bleft(xright)+Cleft(xright)b. Tính giá trị của M(x) khi x-sqrt{0,25}c. Có giá trị nào của x để M(x) 0 không ?
Đọc tiếp
Cho đa thức:
\(A\left(x\right)=2x^5-4x^3+x^2-2x+2\)
\(B\left(x\right)=x^5-2x^4+x^2-5x+3\)
\(C\left(x\right)=x^4+4x3+3x^2-8x+4\frac{3}{16}\)
a. Tính \(M\left(x\right)=A\left(x\right)-2B\left(x\right)+C\left(x\right)\)
b. Tính giá trị của M(x) khi \(x=-\sqrt{0,25}\)
c. Có giá trị nào của x để M(x) = 0 không ?
Bài 1: Cho B = \(x^{2013}-2014x^{2012}+2014x^{2011}-2014x^{2010}+...-2014x^2+2014x-1\)
Tính giá trị của biểu thức B với x=2013.
Bài 2: Cho các số a,b,c khác 0 thỏa mãn: \(\frac{ab}{a+b}=\frac{bc}{b+c}=\frac{ca}{c+a}\)
Tính giá trị của biểu thức : M=\(\frac{ab+bc+ca}{a^2+b^2+c^2}\)
Cho x+ y -2=0 . Tính giá tị các biểu thức sau :
1, A = \(x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
2, B = \(x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
3, C = \(x^3+x^2y-2x^2-x^2y+xy^2+2xy+2y+2x-2\)
TOÁN 7
Giải phương trình
a) \(\frac{4}{20-6x-2x^2}\)+ \(\frac{x^2+4x}{x^2+5x}-\frac{x+3}{2-x}+3=0\)
b)\(\frac{x+5}{x^2-5x}-\frac{x-5}{2x^2-10x}+10=\frac{x+25}{2x^2-50}\)
c) \(\frac{7}{8x}+\frac{5-x}{4x^2-8x}=\frac{x-1}{2x.\left(x-2\right)}+\frac{1}{8x-16}\)
Gọi a là một nghiệm của phương trình
(
26
+
15
3
)
x
+
2
(
7
+
4
3
)
x
-
2
(
2
-
3
)
x
1
. Khi đó giá trị của biểu thức nào sau...
Đọc tiếp
Gọi a là một nghiệm của phương trình ( 26 + 15 3 ) x + 2 ( 7 + 4 3 ) x - 2 ( 2 - 3 ) x = 1 . Khi đó giá trị của biểu thức nào sau đây là đúng?
A. a 2 + a = 2
B. s i n 2 a + cos a = 1
C. 2 + cos a = 2
D. 3 a + 2 a = 5
Cho biểu thức:\(A=1+\left(\frac{2x+\sqrt{x}-1}{1-x}-\frac{2x\sqrt{x}-\sqrt{x}+x}{1-x\sqrt{x}}\right)\frac{x-\sqrt{x}}{2\sqrt{x}-1}\)
a) tìm các giá trị của x để \(A=\frac{6-\sqrt{6}}{5}\)
b)chứng minh rằng \(A>\frac{2}{3}\)với mọi x thỏa mãn \(x\ge0,x\ne1,x\ne\frac{1}{4}\)