Đáp án A.
Đơn vị dài là 2 cm vậy nên đơn vị diện tích quy đổi ra sẽ là 2 2 = 4 c m .
Khi đó S = − 1 2 x 3 d x .4 = 15 c m 2
Đáp án A.
Đơn vị dài là 2 cm vậy nên đơn vị diện tích quy đổi ra sẽ là 2 2 = 4 c m .
Khi đó S = − 1 2 x 3 d x .4 = 15 c m 2
Cho hàm số y = x 2 - m x ( 0 < m < 4 ) có đồ thị (C). Gọi S 1 là diện tích hình phẳng giới hạn bởi (C) và trục hoành; S 2 là diện tích hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x=m,x=4. Biết S 1 = S 2 , giá trị của m bằng
A. 10 3 .
B. 2.
C. 3.
D. 8 3 .
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:

A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
Cho hàm số y=f(x) liên tục trên R và có đồ thị (C) là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường thẳng x=0,x=2 (phần tô đen) là
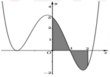
A. S = - ∫ 0 1 f x d x + ∫ 1 2 f x d x
B. S = ∫ 0 1 f x d x - ∫ 1 2 f x d x
C. S = ∫ 0 2 f x d x
D. S = ∫ 0 2 f x d x
Cho hàm số y = f(x) liên tục trên R và có đồ thị (C) là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C) trục hoành và hai đường thẳng x = 0 , x = 2 (phần tô đen) là
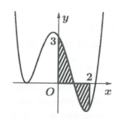
A. S = ∫ 0 1 f x d x - ∫ 1 2 f x d x
B. S = ∫ 0 2 f x d x
C. S = ∫ 0 1 f x d x + ∫ 1 2 f x d x
D. S = ∫ 0 2 f x d x
Đặt (S) là diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 4 - x 2 , trục hoành và đường thẳng x = - 2 , x = m - 2 < m < 2 . Tìm giá trị của tham số m để S = 25 3
A. 2
B. 3
C. 4
D. 1
Cho hàm số
y
=
f
x
=
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây.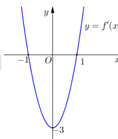 Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
A. S = 9
B. S = 5 4
C. S = 21 4
D. S = 27 4
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho đồ thị ( C ) : y = x . Gọi M là điểm thuộc (C), A(9;0). Gọi S 1 là diện tích hình phẳng giứi hạn bởi (C), đường thẳng x = 9 và trục hoành; S 2 là diện tích tam giác OMA. Tọa độ điểm M để S 1 = 2 S 2 là:
A. M 3 ; 3
B. M(9;3)
C. M(4;2)
D. M 6 ; 6