Ta sẽ vẽ lại hình như sau:
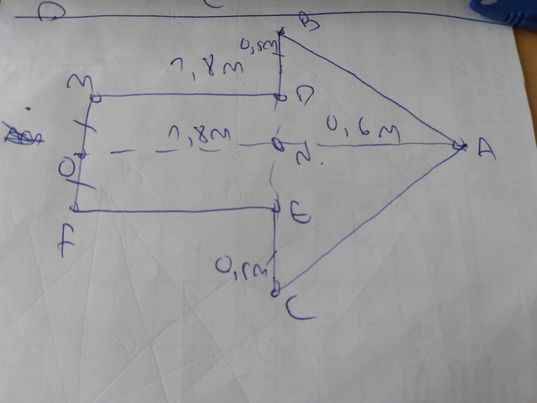
Theo hình, ta có: O là trung điểm của MF
=>OM=OF=MF/2=0,5(m)
=>ND=NE=0,5(m)
BN=BD+DN
=0,5+0,5=1(m)
BN=BD+DN
CN=NE+CE
mà BD=CE và DN=NE
nên BN=CN
=>N là trung điểm của BC
Xét ΔABC có
AN là đường cao
AN là đường trung tuyến
Do đó:ΔABC cân tại A
ΔANB vuông tại N
=>\(AB^2=AN^2+NB^2\)
=>\(AB^2=0,6^2+1^2=1,36\)
=>\(AB=\sqrt{1,36}=\dfrac{\sqrt{34}}{5}\)
=>\(AC=\dfrac{\sqrt{34}}{5}\left(m\right)\)
N là trung điểm của BE
=>\(BE=2\cdot BN=2\left(m\right)\)
Chu vi hình chữ nhật MDEF là \(\left(1,8+1\right)\cdot2=5,6\left(m\right)\)
Chu vi tam giác ABC có \(\dfrac{\sqrt{34}}{5}+\dfrac{\sqrt{34}}{5}+2=\dfrac{2\sqrt{34}+10}{5}\left(m\right)\)
Chu vi của hình là:
\(5,6+\dfrac{2\sqrt{34}+10}{5}=\dfrac{38+2\sqrt{34}}{5}\left(m\right)\)