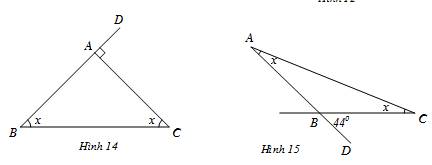
Hình 14:
Ta có:
\(\widehat{BAC}+\widehat{DAC}=180^o\)(Hai góc kề bù)
\(\Rightarrow\widehat{BAC}=180^o-\widehat{DAC}=180^o-90^o=90^o\)
Ta có:
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^o\)(Tổng ba góc trong một tam giác)
\(\Rightarrow90^o+x+x=180^o\)
\(\Rightarrow2x=90^o\)
\(\Rightarrow x=45^o\)
Hình 15:
Ta có:
\(\widehat{ABC}+\widehat{DBC}=180^o\)(Hai góc kề bù)
\(\Rightarrow\widehat{ABC}=180^o-\widehat{DBC}=180^o-44^o=136^o\)
Ta có:
\(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^o\)(Tổng ba góc trong một tam giác)
\(\Rightarrow136^o+x+x=180^o\)
\(\Rightarrow2x=44^o\)
\(\Rightarrow x=22^o\)
#YM
Hình 14:
ΔBAC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(x+x=90^0\)
=>\(2x=90^0\)
=>\(x=\dfrac{90^0}{2}=45^0\)
Hình 15:
Xét ΔBAC có \(\widehat{DBC}\) là góc ngoài tại đỉnh B
nên \(\widehat{DBC}=\widehat{BAC}+\widehat{BCA}\)
=>\(x+x=44^0\)
=>\(2x=44^0\)
=>\(x=22^0\)















 b./
b./  c*./
c*./ 
 b/
b/  =
=  e/
e/  =
=  và
và  e) 9x =81
e) 9x =81 
 h)
h)  và x + y= -21 i)
và x + y= -21 i)  và 3x - 2y = -2
và 3x - 2y = -2 và 3x – 2y – z = -29
và 3x – 2y – z = -29