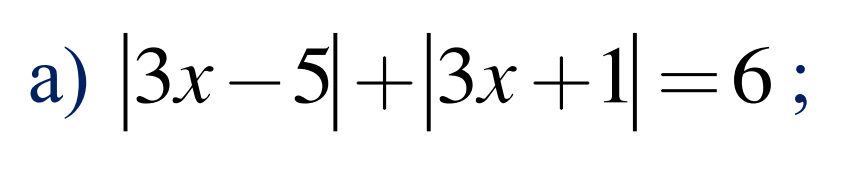TH1: \(x\ge\dfrac{5}{3}\)
\(\left(3x-5\right)+\left(3x+1\right)=6\\ =>3x-5+3x+1=6\\ =>6x-4=6\\ =>6x=6+4\\ =>6x=10\\ =>x=\dfrac{5}{3}\left(tm\right)\)
TH2: \(x\le-\dfrac{1}{3}\)
\(-\left(3x-5\right)-\left(3x+1\right)=6\\ =>-3x+5-3x-1=6\\=>-6x+4=6\\ =>6x=4-6=-2\\ =>x=\dfrac{-2}{6}=-\dfrac{1}{3}\left(tm\right)\)
TH3: \(-\dfrac{1}{3}< x< \dfrac{5}{3}\)
\(-\left(3x-5\right)+\left(3x+1\right)=6\\ =>-3x+5+3x+1=6\\ =>6=6\)
=> \(-\dfrac{1}{3}< x< \dfrac{5}{3}\)
Vậy nghiệm của pt là: `-1/3<=x<=5/3`
\(\left|3x-5\right|+\left|3x+1\right|=\left|5-3x\right|+\left|3x+1\right|>=\left|5-3x+3x+1\right|=6\)
Dấu '=' xảy ra khi (3x-5)(3x+1)<=0
=>\(-\dfrac{1}{3}< =x< =\dfrac{5}{3}\)