Các câu hỏi tương tự
Tìm tất cả các giá trị của tham số m để hàm số
y
(
m
2
-
1
)
x
4
-
2
m
x
2
đồng biến trên khoảng
(
1
;
+
∞
)
A.
m
≤
-
1
B. m -1 hoặc
m
1...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = ( m 2 - 1 ) x 4 - 2 m x 2 đồng biến trên khoảng ( 1 ; + ∞ )
A. m ≤ - 1
B. m = -1 hoặc m > 1 + 5 2
C. m ≤ - 1 hoặc m ≥ 1 + 5 2
D. m ≤ - 1 hoặc m > 1
Tìm tất cả các giá trị thực của tham số m để hàm số
y
log
x
2
−
2
m
x
+
4
có tập xác định là R . A.
m
2
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = log x 2 − 2 m x + 4 có tập xác định là R .
A. m > 2 m < − 2
B. m = 2
C. m < 2
D. − 2 < m < 2
Cho hàm số bậc ba yf(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y|f(x)+m| có ba điểm cực trị là: A.
m
≤
-
1
hoặc
m
≥
3
B.
m
≤
-
3
hoặc
m
≥
1
C. m -1 hoặc m 3 D.
1
≤
m
≤
3
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:
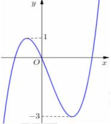
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
Tìm tất cả các giá trị thực của tham số m để hàm số
y
log
2
log
5
m
-
2
2
+
2
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = log 2 log 5 m - 2 2 + 2 m - 3 x + m có tập xác định là ℝ.
A. m≤ 7/3.
B. m >7/3.
C. m ≥7/3.
D. m< 7/3.
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn
5
4
;
4
m
-
1
+
log
1
2
2
x
-
2
2
+
4
m...
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn 5 4 ; 4 m - 1 + log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0
A. m > 7 3
B. - 3 < m < 7 3
C. - 3 ≤ m ≤ 7 3
D. m < - 3
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn
5
4
;
4
m
-
1
+
log
1
2
2
x
-
2
2
+
4
m...
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn 5 4 ; 4 m - 1 + log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0
A. m > 7 3
B. - 3 < m < 7 3
C. - 3 ≤ m ≤ 7 3
D. m < - 3
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
tan
x
-
2
tanx
-
m
xác định trên khoảng
0
;
π
4
A. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = tan x - 2 tanx - m xác định trên khoảng 0 ; π 4
A. m > 1
B. 0 < m < 1
C. m < 0
D. m ≤ 0 hoặc m ≥ 1
Tìm tất cả các giá trị của m để giá trị lớn nhất của hàm số
f
x
2
x
+
m
−
1
x
+
1
trên đoạn [1;2] bằng 1 A. m3 B. m1 C. m0 D. m2
Đọc tiếp
Tìm tất cả các giá trị của m để giá trị lớn nhất của hàm số f x = 2 x + m − 1 x + 1 trên đoạn [1;2] bằng 1
A. m=3
B. m=1
C. m=0
D. m=2
Tìm tất cả các giá trị thực của tham số m để đường thẳng
y
m
cắt đồ thị hàm số
y
x
4
−
2
x
2
−
2
tại 4 điểm phân biệt là A. m-3 B.
−
3
m
−
2
C.
−
3
m
0
D.
3
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số y = x 4 − 2 x 2 − 2 tại 4 điểm phân biệt là
A. m>-3
B. − 3 < m < − 2
C. − 3 < m < 0
D. 3 < m < 0