Đáp án B
TXĐ: D = ℝ .
y ' = 3 x 2 + 6 x = 0 ⇔ 3 x x + 2 = 0 ⇔ x = − 2 x = 0 .
Ta có bảng biến thiên
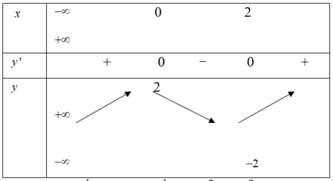
Nhận thấy giá trị nhỏ nhất của hàm số y = x 3 + 3 x 2 + m đạt tại x=0 Ta có y 0 = m = 1.
Vậy m=1 thỏa mãn đề bài.
Đáp án B
TXĐ: D = ℝ .
y ' = 3 x 2 + 6 x = 0 ⇔ 3 x x + 2 = 0 ⇔ x = − 2 x = 0 .
Ta có bảng biến thiên

Nhận thấy giá trị nhỏ nhất của hàm số y = x 3 + 3 x 2 + m đạt tại x=0 Ta có y 0 = m = 1.
Vậy m=1 thỏa mãn đề bài.
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số y = - x 3 - 3 x 2 + m trên đoạn - 1 ; 1 bằng 0.
A. m = 6
B. m = 4
C. m = 0
D. m = 2
Tìm tất cả các giá trị của tham số m để hàm số y = x + m x 2 + x + 1 có giá trị lớn nhất trên ℝ nhỏ hơn hoặc bằng 1.
A. m ≤ 1
B. m ≥ 1
C. m ≥ - 1
D. m ≤ - 1
Tìm tất cả các giá trị thực của tham số m để trên ( - 1 ; 1 ) hàm số y = m x + 6 2 x + m + 1 nghịch biến
A. - 4 < m < 3
B. - 4 ≤ m < - 3 1 < m ≤ 3
C. 1 ≤ m < 4
D. - 4 < m ≤ - 3 1 ≤ m < 3
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x + 6 2 x + m + 1 nghịch biến trên (-1;1)
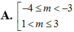
![]()
![]()
Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số y = 1 3 x 3 − m + 1 x 2 + m 2 + 2 m x − 3 nghịch biến trên khoảng (-1;1).
A. S = − 1 ; 0
B. S = ∅
C. S = − 1
D. S = 0 ; 1
Tìm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số y = x + m 2 + 2 x + m 2 − 1 trên đoạn [0;1] bằng 8
A. m = ± 3
B. m = ± 3
C. m = ± 1
D. m = 3
Cho hàm số y = 2 x 3 - 3 m x 2 + 3 ( 5 m 2 + 1 ) x - 3 s i n x với m là tham số thực. Tìm tập hợp tất cả các giá trị của m để hàm số đồng biến trên (l;3).
A . m ≥ 1
B . m ≤ - 1
C . m > 0
D . m ∈ R
Tìm tất cả các giá trị nguyên dương nhỏ hơn 5 của tham số m để hàm số y = 1 3 x 3 + ( m - 1 ) x 2 + ( 2 m - 3 ) x - 2 3 đồng biến trên khoảng (1;+∞)
A. 5
B. 3
C. 6
D. 4