Đáp án A
Phương pháp giải:
Xét các trường hợp của tham số, lập bảng biến thiên để tìm max – min trên đoạn
Lời giải:
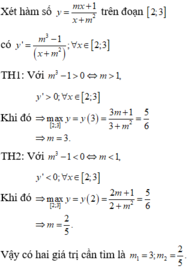
Đáp án A
Phương pháp giải:
Xét các trường hợp của tham số, lập bảng biến thiên để tìm max – min trên đoạn
Lời giải:
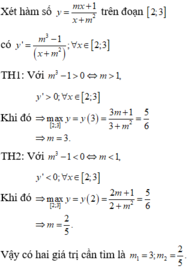
Có tất cả bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y = x 2 − 2 x + m trên đoạn [-1;2] bằng 5.
A. 3
B. 1
C. 2
D. 4
Có tất cả bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số y = x 2 - 2 x + m trên đoạn - 1 ; 2 bằng 5.
A. 3
B. 1
C. 2
D. 4
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số y = f ( x ) = x 3 - ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tất cả các giá trị của tham số m để hàm số y=f(|x|) có 5 điểm cực trị
A. 5 4 < m ≤ 2
B. - 2 < m < 5 4
C. - 5 4 < m < 2
D. 5 4 < m < 2
Tìm tất cả các giá trị của tham số m để hàm số y = x + m x 2 + x + 1 có giá trị lớn nhất trên ℝ nhỏ hơn hoặc bằng 1.
A. m ≤ 1
B. m ≥ 1
C. m ≥ - 1
D. m ≤ - 1
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 2 m + 1 - x + log 3 x - m xác định trên (2;3).
A. -1< m< 2
B. -1≤ m≤ 2
C. 1≤ m≤ 2
D. 1< m≤ 2
Gọi T là tập hợp tất cả các giá trị của tham số m để hàm số y = m x + 1 x + m 2 có giá trị lớn nhất trên đoạn 2 ; 3 bằng 5 6 . Tính tổng của các phần tử trong T.
A. 17 5
B. 2
C. 6
D. 16 5
Gọi S là tổng tất cả các giá trị của tham số m để hàm số y = x 3 + m 2 + 1 x - m + 1 có giá trị lớn nhất trên đoạn 0 ; 1 bằng 9. Giá trị của S bằng
A. S = 5
B. S = -1
C. S = -5
D. S = 1