Hàm số 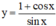 xác định
xác định
⇔ sin x ≠ 0
⇔ x ≠ k.π (k ∈ Z).
Tập xác định của hàm số là D = R \{kπ, k ∈ Z}.
Hàm số 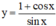 xác định
xác định
⇔ sin x ≠ 0
⇔ x ≠ k.π (k ∈ Z).
Tập xác định của hàm số là D = R \{kπ, k ∈ Z}.
Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó?
y = cot 2x; y = cos(x + π); y = 1 – sin x; y = tan2016x
A. 1.
B. 2
C. 3
D. 4
Tìm tập xác định D của hàm số y = 1 - sin x 1 + sin x
![]()
![]()
![]()
![]()
Tìm tập xác định của các hàm số y = cos x + 1
tìm tập xác định
a) y = cos\(\dfrac{x-1}{x^2-1}\)
b) y = \(sin\sqrt{x}\)
Tập xác định của hàm số y = 1 + cos x 1 - cos x là:
![]()
![]()
![]()
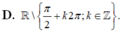
Tìm tập xác định của hàm số sau y = c o t x 2 . sin x - 1
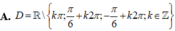
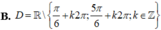
![]()
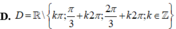
Tập xác định của hàm số y = 1 - cos x sin x - 1 là
![]()
![]()
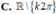
![]()
Tập xác định của hàm số y = 1 - cos x sin x - 1 là:
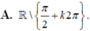
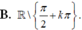
![]()
![]()
Tập xác định của hàm số y = cos x là
A. x > 0
B. x ≥ 0
C. R
D. x ≠ 0 .