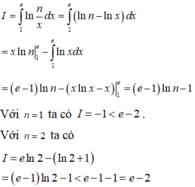Các câu hỏi tương tự
Gọi S là tập hợp số nguyên dương k thỏa mãn điều kiện: ∫ 1 e ln k x d x < e - 2 . Số phần tử của tập S là
A. 2
B. 1
C. 3
D. 0
Xét hàm số
f
(
t
)
9
t
9
t
+
m
2
với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) 1 với mọi số thực x, y thỏa mãn
e
x
+
y...
Đọc tiếp
Xét hàm số f ( t ) = 9 t 9 t + m 2 với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) =1 với mọi số thực x, y thỏa mãn e x + y ≤ e ( x + y ) . Tìm số phần tử của S.
A. 0
B. 1
C. Vô số
D. 2
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
n là số nguyên dương và k là tích của tất cả các số nguyên từ 1 đến n. Nếu k là bội số của 1440 thì giá trị nhỏ nhất có thể có của n là A. 8 B. 12 C. 16 D. 18 E. 24
Cho hàm số f(x) thỏa mãn
f
x
+
f
x
e
-
x
và f(0) 2. Tất cả các nguyên hàm của
f
x
e
2
x
là A. . B. . C. . D. .
Đọc tiếp
Cho hàm số f(x) thỏa mãn f x + f ' x = e - x và f(0) = 2. Tất cả các nguyên hàm của f x e 2 x là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Có tất cả bao nhiêu giá trị của x thỏa mãn đồng thời hai điều kiện x + 1/3 là số nguyên và
log
1
3
5
-
x
log
1
3
3
-
x
? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Có tất cả bao nhiêu giá trị của x thỏa mãn đồng thời hai điều kiện x + 1/3 là số nguyên và log 1 3 5 - x < log 1 3 3 - x ?
A. 1
B. 2
C. 3
D. 4
Cho F(x) là một nguyên hàm của hàm số
1
e
x
+
1
, thỏa mãn F(0) –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) 3. A.
S
3
B.
S
-
3
C.
S...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F(0) = –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) = 3.
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Tính các nguyên hàm.
a)\(\int\dfrac{2dx}{x^2-5x}=A\ln\left|x\right|+B\ln\left|x-5\right|+C\) . Tìm 2A-3B.
b)\(\int\dfrac{x^3-1}{x+1}\)dx=\(Ax^3-Bx^2+x+E\ln\left|x+1\right|+C\).Tính A-B+E
Cho
f
(
n
)
(
n
2
+
n
+
1
)
2
∀
n
∈
N
*
Đặt
u
n
f
(...
Đọc tiếp
Cho f ( n ) = ( n 2 + n + 1 ) 2 ∀ n ∈ N * Đặt u n = f ( 1 ) . f ( 3 ) . . . f ( 2 n - 1 ) f ( 2 ) . f ( 4 ) . . . f ( 2 n ) .
Tìm số n nguyên dương nhỏ nhất sao cho u n thỏa mãn điều kiện log 2 u n + u n < - 10239 1024 .
A. n=23
B. n=29
C. n=21
D. n=33