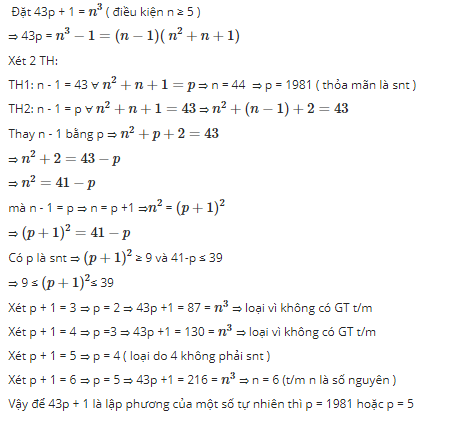Question

Tìm số nguyên tố p sao cho 43p+1 là lập phương của một số tự nhiên.

Answer 1

Tham khảo:

Answer 2

Đặt `43p + 1 = n^3 ( n in NN)`

`=> 43p = (n-1)(n^2 + n+1)`

`+ n - 1 = 43 => n = 44 => n^2 + n + 1 = p => p = 1981`.

`+ n - 1 = p => n^2 + p + 2 = 43`

`=> n^2 + p = 41`

Mà `n^2 = (p-1)^2`

`=> (p-1)^2 = 41 - p`

`+)` Chặn: `9 <= (p+1)^2 <=39`

`=> (p+1)^2 in {9, 16, 25, 36}`

Xét `4` trường hợp, nhận thấy chỉ có `(p+1)^2 = 36 => p = 5` thỏa mãn yêu cầu.

Vậy `p = 1981, 5`.