Đáp án C
Số giao điểm với trục hoành là số nghiệm của phương trình
![]()
Đáp án C
Số giao điểm với trục hoành là số nghiệm của phương trình
![]()
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số y=f(x) xác định trên R. Đồ thị hàm số y = f ' ( x ) cắt trục hoành tại 3 điểm a, b, c ( a < b < c ) như hình dưới:
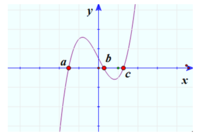
Biết f(b) < 0 Đồ thị hàm số y=f(x) cắt trục hoành tại bao nhiêu điểm phân biệt.
A. 4
B. 1
C. 0
D. 2
Số giao điểm của đồ thị hàm số y = x - 1 x 2 + 2 x - 3 với trục hoành là
A. 1
B. 2
C. 3
D. 0
Biết đồ thị hàm số bậc bốn y=f(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số y=g(x)= [f’(x)]2 – f(x). f’’(x) và trục hoành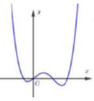
A. 4
B. 0.
C. 6.
D. 2.
Gọi M là giao điểm của đồ thị hàm số y = x + 1 x − 2 với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là:
A. 3 y + x + 1 = 0
B. 3 y + x − 1 = 0
C. 3 y − x + 1 = 0
D. 3 y − x − 1 = 0
Gọi M là giao điểm của đồ thị hàm số y = x + 1 x − 2 với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là
A. 3 y + x + 1 = 0
B. 3 y + x − 1 = 0
C. 3 y − x + 1 = 0
D. 3 y − x − 1 = 0
Tìm số giao điểm của đồ thị hàm số y = x - 1 x 2 - 2 x với trục hoành.
A. 1
B. 2
C. 0
D. 3
cho hàm số \(y=x^2\) và y = -2x+3
a, Vẽ đồ thị của hàm số trên cùng 1 hệ trục tọa độ.
b, Tìm tọa độ giao điểm của 2 đồ thị đó.
Tìm hệ số góc tiếp tuyến k của đồ thị hàm số y = x + 2 1 − x tại giao điểm của nó với trục hoành.
A. k = − 3
B. k = − 1 3
C. k = 1 3
D. k = 3