Các câu hỏi tương tự
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Tìm số giao điểm của đồ thị hàm số y = ( x − 2 ) ( x 2 + 3 x + 3 ) với trục hoành.
A. 2
B. 0
C. 1
D. 3
Biết đồ thị hàm số bậc bốn yf(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số yg(x) [f’(x)]2 – f(x). f’’(x) và trục hoành A. 4 B. 0. C. 6. D. 2.
Đọc tiếp
Biết đồ thị hàm số bậc bốn y=f(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số y=g(x)= [f’(x)]2 – f(x). f’’(x) và trục hoành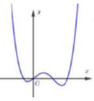
A. 4
B. 0.
C. 6.
D. 2.
Cho hàm số yf(x) xác định trên R. Đồ thị hàm số
y
f
(
x
)
cắt trục hoành tại 3 điểm a, b, c (
a
b
c
) như hình dưới: Biết f(b) 0 Đồ thị hàm số yf(x) cắt trục hoành tại bao nhiêu điểm phân biệt. A. 4 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y=f(x) xác định trên R. Đồ thị hàm số y = f ' ( x ) cắt trục hoành tại 3 điểm a, b, c ( a < b < c ) như hình dưới:
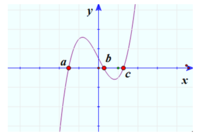
Biết f(b) < 0 Đồ thị hàm số y=f(x) cắt trục hoành tại bao nhiêu điểm phân biệt.
A. 4
B. 1
C. 0
D. 2
Gọi M là giao điểm của đồ thị hàm số
y
x
+
1
x
−
2
với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là: A.
3
y
+
x
+
1
0
B.
3
y
+
x
−
1
0
C.
3...
Đọc tiếp
Gọi M là giao điểm của đồ thị hàm số y = x + 1 x − 2 với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là:
A. 3 y + x + 1 = 0
B. 3 y + x − 1 = 0
C. 3 y − x + 1 = 0
D. 3 y − x − 1 = 0
Gọi M là giao điểm của đồ thị hàm số
y
x
+
1
x
−
2
với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là A.
3
y
+
x
+
1
0
B.
3
y
+
x
−
1
0
C.
3...
Đọc tiếp
Gọi M là giao điểm của đồ thị hàm số y = x + 1 x − 2 với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là
A. 3 y + x + 1 = 0
B. 3 y + x − 1 = 0
C. 3 y − x + 1 = 0
D. 3 y − x − 1 = 0
Số giao điểm của đồ thị hàm số
y
x
-
1
x
2
+
2
x
-
3
với trục hoành là A. 1 B. 2 C. 3 D. 0
Đọc tiếp
Số giao điểm của đồ thị hàm số y = x - 1 x 2 + 2 x - 3 với trục hoành là
A. 1
B. 2
C. 3
D. 0
Tìm hệ số góc tiếp tuyến k của đồ thị hàm số
y
x
+
2
1
−
x
tại giao điểm của nó với trục hoành. A.
k
−
3
B.
k
−
1
3
C.
k
1
3
D.
k...
Đọc tiếp
Tìm hệ số góc tiếp tuyến k của đồ thị hàm số y = x + 2 1 − x tại giao điểm của nó với trục hoành.
A. k = − 3
B. k = − 1 3
C. k = 1 3
D. k = 3
Cho hàm số
y
x
−
2
x
+
1
. Xét các phát biểu sau đây+) Đồ thị hàm số nhận điểm
I
−
1
;
1
làm tâm đối xứng.+) Hàm số đồng biến trên tập
ℝ
−
1
.+) Giao điểm của...
Đọc tiếp
Cho hàm số y = x − 2 x + 1 . Xét các phát biểu sau đây
+) Đồ thị hàm số nhận điểm I − 1 ; 1 làm tâm đối xứng.
+) Hàm số đồng biến trên tập ℝ \ − 1 .
+) Giao điểm của đồ thị với trục hoành là điểm A 0 ; − 2
+) Tiệm cận đứng là y = 1 và tiệm cận ngang là x = − 1
Trong các phát biểu trên, có bao nhiêu phát biểu đúng?
A. 1
B. 3
C. 2
D. 4