Chọn A
y ' = 3 x 2 - 6 x + m .
Hàm số có cực trị khi y' = 0 có hai nghiệm phân biệt :

Chọn A
y ' = 3 x 2 - 6 x + m .
Hàm số có cực trị khi y' = 0 có hai nghiệm phân biệt :

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S m ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - m ) 2 = m 2 4 và hai điểm A(2;3;5), B(1;2;4). Tìm giá trị nhỏ nhất của m để trên ( S m ) tồn tại điểm M sao cho M A 2 - M B 2 = 9 .
A. m=1
B. m= 3 - 3
C. m= 8 - 4 3
D. m= 4 - 3 2
cho (Cm) y=2x^3-3(2m+1)x^2+6m(m+1)x-2m^3
Tìm m để (Cm) cắt trục Ox tại 3 điểm phân biệt
Tìm tất cả giá trị của m để hàm số y = 1/3.x3 – mx2 + (m2 – m + 1)x + 1 đạt cực đại tại x = 1
A. m = -2
B. m = -1
C. m = 2.
D. m = 1
Tìm m để hàm số y = - x 3 + ( 2 m + 1 ) x 2 - ( m 2 - 3 m + 2 ) x - 4 có cực đại, cực tiểu nằm về hai phía so với trục tung
A. m ∈ (1; 2)
B. m ∈ [1; 2]
C. m ∈ (- ∞; 1) ∪ (2; +∞)
D. m ∈ (- ∞; 1] ∪ [2; +∞)
Tìm m để đồ thị hàm số y = x 3 + 3 x 2 + m x + 2 m cắt đường thẳng y = -x + 2 tại 3 điểm.
A. m > 5 4
B. m > 1
C. m < 5 4 và m ≠ - 1
D. - 1 < m < 5 4
Cho hàm số y = f(x) thỏa mãn f(-2) = -2, f(2) = 2 và có bảng biến thiên như hình bên
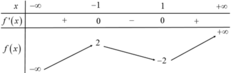
Có bao nhiêu số tự nhiên m thỏa mãn bất phương trình f - f x ≥ ≥ m có nghiệm thuộc đoạn [-1;1]?
A. 1.
B. 2.
C. 3.
D. 4.
Hàm số nào sau đây không có cực trị
A: \(y=\dfrac{x^2+1}{x}\)
B: \(y=\dfrac{2x-x}{x+1}\)
C: \(y=x^2-2x+1\)
D: \(y=-x^3+x+1\)
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
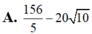
![]()
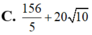
![]()
Hàm số y = x 3 + (m + 3) x 2 + mx - 2 đạt cực tiểu tại x = 1 khi:
A. m = 1 B. m = 2
C. m = -3 D. m = 4