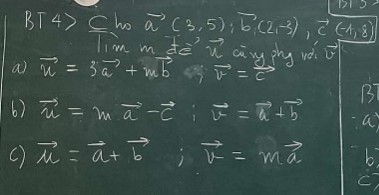a: \(\overrightarrow{u}=3\cdot\overrightarrow{a}+m\cdot\overrightarrow{b}\)
=>\(\left\{{}\begin{matrix}x_u=3\cdot3+m\cdot2=2m+9\\y_m=3\cdot5+m\cdot\left(-3\right)=-3m+15\end{matrix}\right.\)
\(\overrightarrow{v}=\overrightarrow{c}\)
=>\(\overrightarrow{v}=\left(-1;8\right)\)
Để \(\overrightarrow{u}\) cùng phương với \(\overrightarrow{v}\) thì \(\dfrac{2m+9}{-1}=\dfrac{-3m+15}{8}\)
=>8(2m+9)=3m-15
=>16m+72=3m-15
=>13m=-87
=>\(m=-\dfrac{87}{13}\)
b: \(\overrightarrow{u}=m\cdot\overrightarrow{a}-\overrightarrow{c}\)
=>\(\left\{{}\begin{matrix}x_u=m\cdot3-\left(-1\right)=3m+1\\y_u=m\cdot5-8=5m-8\end{matrix}\right.\)
\(\overrightarrow{v}=\overrightarrow{a}+\overrightarrow{b}\)
=>\(\left\{{}\begin{matrix}x_{\overrightarrow{v}}=3+2=5\\y_{\overrightarrow{v}}=5+\left(-3\right)=2\end{matrix}\right.\)
Để \(\overrightarrow{u};\overrightarrow{v}\) cùng phương thì \(\dfrac{3m+1}{5}=\dfrac{5m-8}{2}\)
=>5(5m-8)=2(3m+1)
=>25m-40=6m+4
=>19m=44
=>\(m=\dfrac{44}{19}\)
c: \(\overrightarrow{u}=\overrightarrow{a}+\overrightarrow{b}\)
=>\(\overrightarrow{u}=\left(5;2\right)\)
\(\overrightarrow{v}=m\cdot\overrightarrow{a}\)
=>\(\left\{{}\begin{matrix}x_{\overrightarrow{v}}=m\cdot3=3m\\y_{\overrightarrow{v}}=5m\end{matrix}\right.\)
Để hai vecto u và v cùng phương thì \(\dfrac{3m}{5}=\dfrac{5m}{2}\)
=>m=0